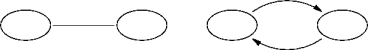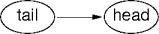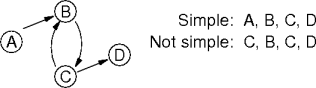Computer Algorithms II Lecture Notes

6 November 2008 • Graph Basics

Outline

• Some problems.

• Terminology

• Graph Data Structures.

• Graph Traversals.

• Graph Implementations.

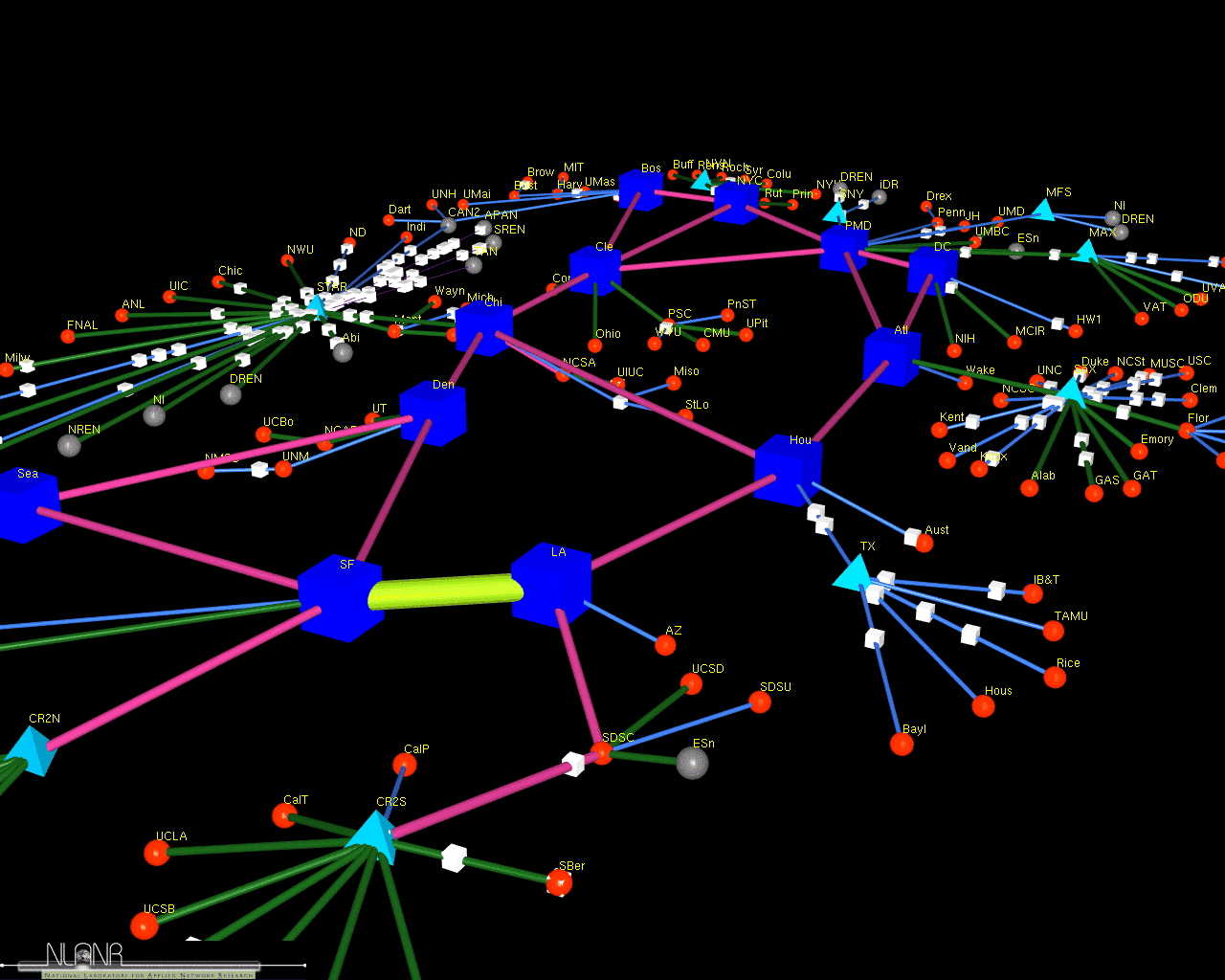
Route Finding

• A more recent, fuller map.

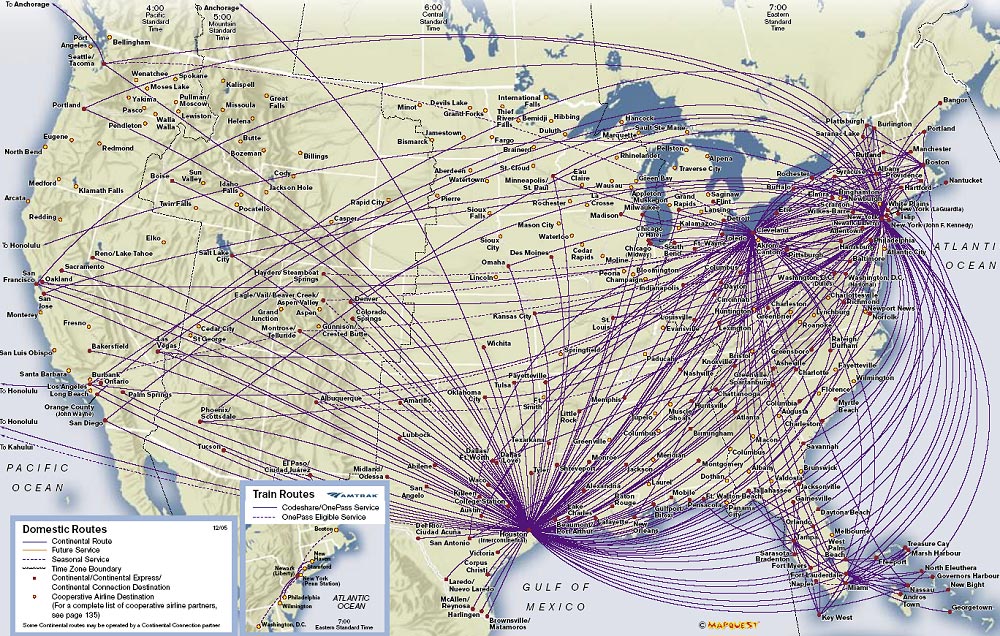
Traffic Scheduling

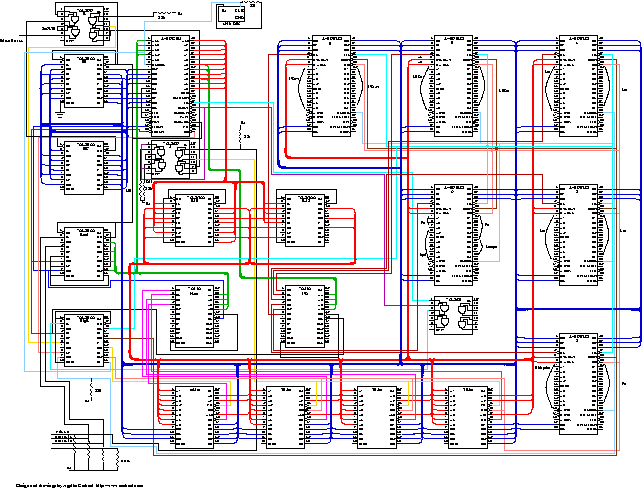
Schematic Analysis

Graphs

• All these problems - and more - can be solved with graphs.

• Graphs can

  • model the problems, and

  • provide algorithms to find solutions.

• The generality with which graphs do these things makes them useful and important.

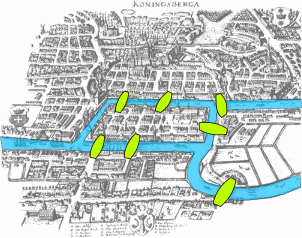
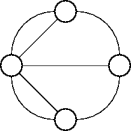
The Königsberg Bridges

The Bridges Problem

• Is it possible to walk all seven bridges once?

• Leonhard Euler answered the question in 1735.

  Model each land mass as a point. Model each bridge as a connection between points.

• A parity argument shows it’s impossible.

  • Such a walk is a Euler path.

Graph Terminology

• A graph G is a set of vertices V and a set of edges E between the vertices in V.

  • Either of V or E may be empty.

  • Because V and E are sets, they contain no duplicates.

  • Vertices are sometimes nodes; edges are sometimes arcs or links.

• Trees are a special-case of graphs.

  • A tree is a connected acyclic graph.

Graph Labels

• Vertices and edges may have labels.

  

  • The graph is known as a labeled graph

• Numeric edge labels are called weights.

  

  • The edges are weighted edges and the graph is a weighted graph.

Graph Models

• When modeling, graph vertices represent entities and edges represent relations between entities.

  • Vertices can represent Internet routers, terminal cities, electronic components, or land masses.

  • Edges can represent networks between routers, flights between cities, wires between components, or bridges between land masses.

Graph Data Structures

• Graph data structures tend to be complex.

  • Graphs are complex and open ended.

  • Graphs models can be complex.

  • Graph algorithms can be complex.

  • And then there’s efficiency and convenience.

• Graph data structures tend towards the extremes.

  • Either minimal or specialized data strctures.

Graph Traversal

• A graph traversal is an algorithm that visits vertices in a graph.

• Traversals are necessary for searching a graph.

• The main idea is to follow edges from one vertex to the next.

  • The result is a sequence of vertices visited: V₁, V₂, V₃, ...

• Different traversals produce vertex sequences with different properties.

More Graph Terms

• A directed graph (digraph) has directed edges.
• An undirected edge allows two-way traversal.

  • An undirected edge is a pair of directed edges.

    

Paths

• A path between vertices v₁ and v_n, n ≥ 1, is a sequence of vertices v₁, v₂, ..., v_n such that

  • The edge (v_i, v_{i + 1}) exists for 1 ≤ i < n.

• The path length is n - 1 (the number of edges).

  • Paths may have arbitrary length (n > |V|).

• Traversals produce paths.

Adjacency

• Two vertices are adjacent if they’re connected by an edge.

  • Adjacency follows a directed edge.

    

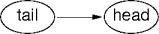
• Two vertices are neighbors if they’re adjacent.

Basic Traversal

• The basic idea behind traversal is:

  1. Get all neighbors of the current vertex.

  2. Pick one of the neighbors and make it current.

• Traversal algorithms differ in

  1. how neighbors are selected, and

  2. how the new current vertex is selected.

One-Visit Assumption

• Each vertex should be visited at most once.

• This requires either

  • a visited bit in each vertex or

  • the algorithm keep track of visited vertices itself.

• Selecting neighbors inolves finding all unvisited neighbors.

Random Traversal

rt(graph g, vertex current)

  set pending-visits(current)

  while not pending-visits.empty()
    current = pending-visits.pick()
    current.visited = true
    for each n in g.neighbors(current)
      if n not in pending-visits 
         and not n.visited
	pending-visits.add(n)

• Note the graph query operator neighbors().

Graph Traversal Properties

• The graph traversal is discontinuous.

  • It follows edges until there aren’t any more.

  • Then it jumps back to a pending vertex (if any).

  • The jumps are known as backtracking.

  

Graph Algorithm Performance

• The two main performance parameters for a graph are

  1. The number of vertices |V|.

  2. The number of edges |E|.

• Graph operator performance depends on implementation details.

Random Traversal Peferformance

set pending(current)          O(1)
while not pending.empty()     O(1)×O(|V|)
  current = pending.pick()    O(1)
  nbrs = g.neighbors(current) O(|V|)
  for each n in nbrs          O(1)×O(|V|)
    if not n.visited          O(1)
      n.visited = true        O(1)
      pending.add(n)          O(log |E|)

• A rough accounting gives O(|V|²log |E|).

• A finer accounting gives O(|V| + |E|).

A Simple Problem

• Given a graph G and a vertex v in G, find another vertex v' in G that is one of the vertices closest to v that satisfies a prediate p().

  • Vertex distance is path length.

  

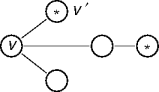
• Randomly backtracking isn’t going to solve this problem.

Ordered Backtracking

• Backtrack to a vertex closest to v.

  • The children, and then the grandchildren, and then ...

• The first neighbers found should be the first vertices backtracked to.

• First in, first out - queue pending neighbors.

  

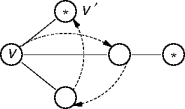
Breadth-First Traversal

vertex bft(graph g, vertex current)

  queue pending-visits(current)

  while not pending-visits.empty()

    current = pending-visits.deq()
    current.visited = true

    for each n in g.neighbors(current)
      if p(n) return n
      if n not in pending-visits 
         and not n.visited
	pending-visits.enq(n)

Cycles

• A cycle (or circuit) is a path in which v₁ = v_n.

  • The path should have at least one edge.

  • An Euler circuit is an Euler path that ends where it started.

• A graph with no cycles is acyclic.

• A path with no cycles is a simple path.

  

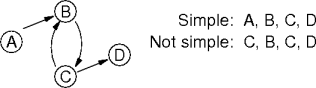
Another Simple Problem

• Given a graph G determine if G contains a cycle.

• A path with a cycle contains repeated vertices.

  • Visiting an already visited vertex.

• Random or breadth-first backtracking jump around too much.

• The next vertex to visit should be one of the most recent neighbors found.

• Last in, first out - use a stack

Depth-First Traversal

bool dft(graph g, vertex current)

  stack pending-visits.push(current)

  while not pending-visits.empty()

    current = pending-visits.pop()
    current.visited = true

    for each n in g.neighbors(current)
      if n in pending-visits or n.visited
        return true
      pending-visits.push(n)

  return false

Graph Data Structures

• Stick with the basics, extended for vertices and edges.

  • Don’t forget labels and directedness.

• Create and delete graphs, vertices, and edges.

• Add and remove operations for vertices and edges.

• All manner of search operations, including depth- and breadth-first searches.

Adjacency Matrix

• A |V|×|V| boolean matrix indexed by vertices.

  

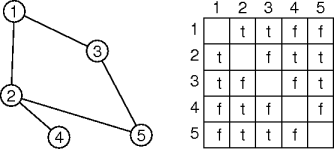
• An undirected graph can use a-half diagonal matrix.

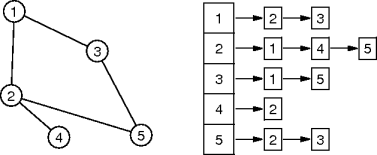
Edge Lists

• Adjacency matrices are wasteful with few (or many) edges.

  • Slice along the rows (or columns).

  • Keep only the true (or false) entries.

  

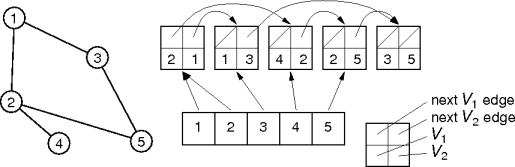
Vertex Lists

• Edge lists waste half their space for undirected graphs.

  • Share the edge nodes (doubling their size).

  • Thread the vertices through the edges.

  

Graph Data Structures

• The Graph Template Library.

• The Boost Graph Library.

  • There’s also a parallel version.

• The Adaptave Graph Library, which adjusts implementations based on applied operations.

• A specialized SUIF library for representing control-flow graphs used in compilers.

Summary

• Graphs represent relations between things.

  • Relations are edges, things are vertices.

• Graphs are a general modeling tool.

  • There are lots of graph-like things.

  • Lots of things can be modeled as graphs.

• There’s a huge catalog of graph algorithms available for use.