Computer Algorithms II Lecture Notes

13 November 2008 • Graph Algorithms

Outline

Connected Graphs
- Articulation Points
- Biconnectedness
Spanning Trees
- Minimum Spanning Trees
PERT Charts

Connectedness

An undirected graph is connected if there is a path between any two vertices.
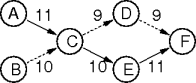
- The connected parts are called components
A directed graph is strongly connected if there is a path between any two vertices.

Connected Graphs

It's often important that a graph be connected.
- Networks, highway systems.
It's often important that a graph be unconnected.
- Security models.
Given a graph G, how can you determine if it's connected?

Connectedness Algorithm

A graph is connected if a traversal touches every node.

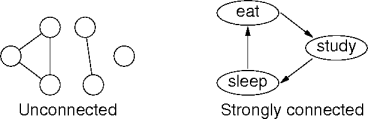
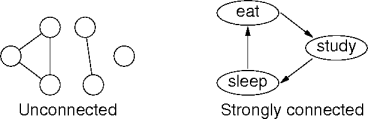
bool connected(graph g)
  return g.vertices().size() = 
           visit(g, g.vertices().pick())

int visit(graph g, vertex v)
  if not v.visited
    cnt = 1
    v.visited = true
    for n in g.neighbors(v)
      cnt += visit(g, n)
  return cnt

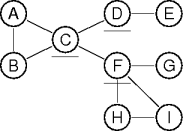
Articulation Points

A vertex V in a connected graph G is an articulation point if removing V splits G into two or more components.
- Removing an articulation point disconnects the graph.

Biconnectedness

A graph is biconnected if it has no articulation points.
- Removing any vertex leaves the graph connected.
If it's important that a graph be connected, it's usually important that it remain connected.
Given a graph, is it biconnected?

Depth-First Searching

Children without backedges can be disconnected.
- The root is a special case.

Recognizing Backedges

backedges

A backedge must go from a descendant to an ancestor
- This requires more than one bit.
Assign each node a depth based on the predecessor node's depth.
The backedge target must have a depth less than the root node.

A Biconnectedness Algorithm

bool biconnected(graph g)
  root = g.vertices().pick()
  root.depth = 0
  return root.neighbors().size() < 2 and
    is_biconnected(g, root)

bool is_biconnected(graph g, vertex v)
  min-depth = v.depth
  for n in g.neighbors(v)
    if n.depth > -1
     min-depth = min(min-depth, n.depth)
    else
     n.depth = v.depth + 1
     if not is_biconnected(g, n)
       return false 
  return min-depth < v.depth

Spanning Trees

Given a connected graph G, a spanning tree of G is a tree T with
- V_T = V_G and E_T ⊆ E_G
A spanning tree is plan for traversal.
- Multicast delivery in networks.
- Multiple spanning trees provide biconnectedness.
Given a graph, find a spanning tree.

Spanning Tree Example

example spanning trees

Why do the red edges form a tree?
- Acyclic
- Connected

A Spanning-Tree Algorithm

Either search produces spanning trees.

graph spanning_tree(graph g)
  queue unvisited(g.vertices().pick())
  t.add_vertex(unvisited.head())    
  while not unvisited.empty()
    v = unvisited.deq()
    for n in g.neighbors(v)
      if not t.vertices().member(n)
        t.add_vertex(n)
        t.add_edge(v, n)
	unvisited.enq(n)
  return t

Traversal Costs

Edge traversals may have costs.
- Miles traveled, transmission speed.
A weighted graph can represent traversal costs.
- The G.weight(e) query operation returns the weight associated with edge e.
Given a weighted graph G find a cheapest spanning tree for G considering the sum of all edge costs.

Minimum Spanning Trees

Given a weighted graph G, a minimum spanning tree (MST) for G is a spanning tree T for G such that for any other spanning tree T' of G,
- sum(T.weight(T.edges())) ≤ sum(T'.weight(T'.edges()))
Given a weighted graph G find a minimum spanning tree for G.

Example Non-MST

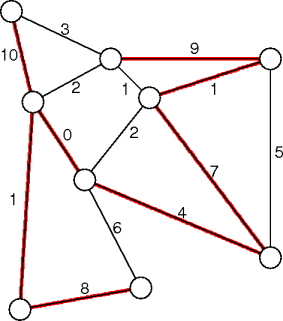
example non-minimal spanning trees

Finding MSTs

a simple weighted graph

Straight depth- or breadth-first searching don't discriminate among edges.

Modify the search algorithms to always chose the neighbor along the cheapest edge.
- That is, replace the queue or stack with a min-priority queue.
- Add edges with weight priority to the queue.

An MST Algorithm

graph mst(graph g)

  min-queue minq
  graph mst
  vertex v = g.vertices().pick()

  for n in g.neighbors(v)
    minq.enq((v, n), g.weight(v, n))
  while not minq.empty()
    e = minq.deq()
    v = e.second()
    if not mst.vertices().member(v)
      mst.add_edge(e)
      for n in g.neighbors(v)
	if not mst.vertices().member(n)
	  minq.enq((v, n), g.weight(v, n))

  return mst

Example MST

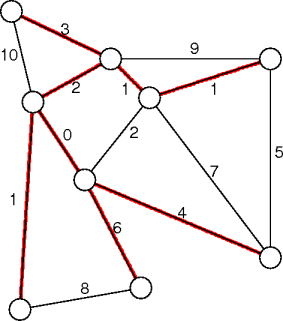
example minimal spanning trees

MST Algorithm Properties

Always adding the cheapest edge produces a minimum spanning tree.
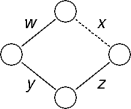
mst() has O((V + E)log V) running time.
This algorithm is known as priority first search (pfs).

Path Weights

Let G be a weighted graph and P a path through G.
The path weight of P is the sum of the weights of the edges in P.
Given a weighted graph G and vertices v_s and v_e in G, find a minimum-weight path from v_s to v_e.

Finding Minimum Paths

Does an MST rooted at v_s find minimum paths?
Pfs extends the entire tree by the cheapest pending edge.
- The cheapest edge in an MST may not be the cheapest edge in a path from v_s to v_e

Modified PFS

Add edges based on their effect on the path weights from v_s.
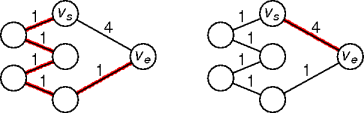
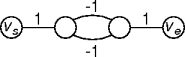
Maintain an auxiliary array dist.
- dist[v_i] is the weight of the minimum path from v_s to v_i.
- Add an edge only if it results in a cheaper path from v_s.

A Minimum-Path Algorithm

min-path(graph g, vertex v_s)
  unsigned dist[g.vertices().size()] = { ∞ }
  min-queue minq
  for n in g.neighbors(v_s)
    dist[n] = g.weight(v_s, n)
    minq.enq((v_s, n), g.weight(v_s, n))

  while not minq.empty()
    e = minq.deq()
    v = e.second
    if dist[v] > dist[e.first] + g.weight(e)
      dist[v] = dist[e.first] + g.weight(e)
      for n in g.neighbors(v)
	if not n mst.vertices().member(n)
	  minq.enq((v,n),dist[v]+g.weight(v,n))

Min-Path Properties

This algorithm finds all minimum paths from v₁.
Always adding the cheapest edge produces minimum paths.
min-path() has O((V + E)log V) running time.
This algorithm is known as Dijkstra's min-path algorithm.

Observations

Dijkstra’s algorithm fails for graphs with negative cycles.
The algorithm only gives the lengths, not the paths themselves.
- Use the vertex array parent.
- To go from v_s to v_e, go from v_s to parent[v_e] and then take (parent[v_e], v_e).

PERT Charts

A PERT chart is a weighted, directed graph that models a project.
- The vertices are tasks.
- A tail tasks must be completed before a head task can start.
- The edge weight gives the tail-task duration.

Directed Acyclic Graphs

A PERT chart can’t have any cycles.
- Do task 1 before task 2, and task 2 before task 1.
A PERT chart is an example of a directed acyclic graph (dag).
A dag has more structure than a tree (vertices can be shared)
- And less structure than a directed graph (no cycles).

Scheduling PERT Tasks

Given a PERT chart, find a schedule (a list) of tasks respecting the task order.
A breadth-first search doesn’t do the job.
Depth-first search neither.

Depth-first search backtracks more coherently then does breath-first search.

Although the backtracking is in reverse order.
D, E, C, B, A

PERT-Schedule Algorithm

list
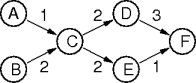
pert-sched(graph g, vertex v)
  return
    sched(g, v, list.create()).reverse()

list
sched(graph g, vertex v, list l)
  if not v.visited
    v.visited = true
    for n in g.neighbors(v)
      sched(g, n)
  return l.add(v)

Exploiting Independence

The task list A, B, C, D is wasteful for the PERT chart
Tasks B and C are independent and can be done at the same time after A is done.
A better task list is A, { B, C }, D
- { T₁, T₂, ... } means "Do tasks T₁, T₂, ... at the same time".
How to produce better paths?

Edge And Vertex Terms

An in-edge points into into a vertex; an out-edge points away from a vertex.
A vertex’s in-degree equals the number of the vertex’s in-edges.
- Similarly for a vertex’s out-degree.
A 0 in-degree vertex is a root (input, source).
A 0 out-degree vertex is a leaf (output, sink).

Producing Better Schedules

list
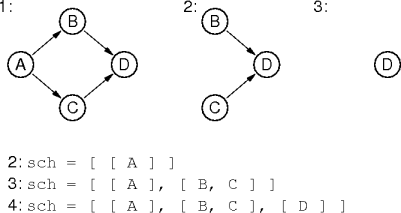
schedule(graph g)
  list sch
  while g.vertices().size() > 0
    list tier
    for n in g.vertices()
      if g.in_degree(n) = 0
        tier.add(n)
	g.remove(n)
    sch.add(tier)
  return sch

Example Schedule

an example schedule

Critical Paths

A critical path through a PERT chart is a path of maximum weight from an input to an output vertex.
Task-completion delays along the critical path causes schedule skip.
- Non-critical path tasks have slack.
  - They can tolerate a bounded amount of task-completion delay.

Finding Critical Paths

An inverted Dikjstra’s algorithm will find critical paths.
Either
- change the min-queue to a max-queue, or
- Subtract the edge weights from a large value (the sum of all task durations, say).

Summary

Look at depth-first and breadth-first searches.
- If they don’t work, figure out why and modify them.
Graphs can have lots of tricky special cases.
- Impose as much structure on the graph as you can.
Learn graph theory.
- Somebody’s probably been there before.

This page last modified on 20 November 2008.