Computer Algorithms II Lecture Notes

4 November 2008 • Greed in Practice

Outline

• Exact solutions.

  • Huffman encoding.

• Approximate solutions.

  • Vertex cover.

  • Non-optimality bounds.

• Heuristics.

  • Repetition

  • Local optimizations.

Encoding Symbols

• Given a set S = { s₀, s₁, …, s_n-1 } of symbols, encode the symbols as binary strings.

  • Example: S = { ♁, ♃, ☿, ♆, ♇, ♄, ♅ }

    s:	☿	♁	♃	♄	♅	♆	♇
    E(s):	000	001	010	011	100	101	110

• A set of n symbols can be encoded as ⌈log₂n⌉-bit numbers.

Encoding Strings

• Let s be a string over the symbols in S.

• If E is an encoding for S, E can encode s symbol by symbol.

  E(♁ ♄ ♃ ♁ ♇) = 000011010000110

• The encoded string is |s|⌈ log₂ n⌉ bits long.

• Can we do better? Can we encode s in fewer bits?

Symbol Frequencies

• Suppose ♁ is ten times more likely to appear in strings than the other symbols.

• Represent ♁ with one bit, the rest of the symbols with three bits.

  • This is a variable-length encoding.

• For a string of n symbols,

  • Constant encoding size is 3n.

  • Variable encoding size is n*0.1*1 + n*0.9*3 = 2.8n.

Frequency-Based Encoding

• Symbol-encoding size is inversly proportional to symbol frequency.

  • Frequent symbols have short encodings (fewer bits).

• The two problems are now:

  • How should the symbols and their frequencies be arranged?

  • How should the symbols be encoded?

Huffman Tree

• A Huffman tree over a symbol set S is a full binary tree.

• Each leaf corresponds to a symbol frequency.

• An interior node's frequency is the sum of its children's frequencies.

• Tree-node levels are inversly proportional to frequency.

  • High frequency nodes have low levels.

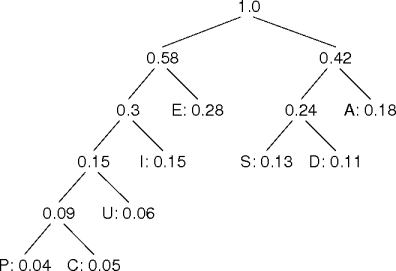
Huffman Tree Example

E 0.28 A 0.18 I 0.15 S 0.13 D 0.10 U 0.06 C 0.05 P 0.04

Huffman Encoding

• Symbols in a Huffman tree are easily encoded:

  • Start at the root with an empty string.

  • Append a 0 (or 1) to the string on each move to a left child.

  • Append a 1 (or 0) to the string on each move to a right child.

  • A leaf is encoded by the string.

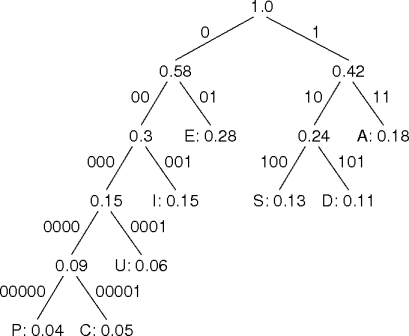
Huffman Encoding Example

E 01 A 11 I 001 S 100 D 101 U 0001 C 00001 P 00000

Does It Work?

• Eight symbols can be encoded with 3 bits.

• A string with n symbols is encoded with 3n bits.

• The Huffman-encoded string takes

  	(0.27 + 0.17)2 + (0.15 + 0.13 + 0.10)3 + 0.06*4 + (0.05 + 0.04)5
  =	0.44*2 + 0.38*3 + 0.06*4 + 0.9*5
  =	0.88 + 1.14 + 0.24 + 0.45
  =	2.71 bits/symbol

Creating Huffman Trees

• The two smallest symbol frequencies should be furthest from the root.

  • Combine as the children of a parent.

  • The parent's frequency is the sum of its childrens' frequencies.

  • The parent represents a new pseudo-symbol.

• Repeat until there's one symbol left.

  • This is a greedy algorithm.

Example

E	A	I	S	D	U	C	P
0.28	0.18	0.15	0.13	0.11	0.06	0.05	0.04
E	A	I	S	D	CP	U
0.28	0.18	0.15	0.13	0.11	0.09	0.06
E	A	I	CPU	S	D
0.28	0.18	0.15	0.15	0.13	0.11
E	SD	A	I	CPU
0.28	0.24	0.18	0.15	0.15
ICPU	E	SD	A
0.30	0.28	0.24	0.18
SDA	ICPU	E
0.42	0.30	0.28
ICPUE	SDA
0.58	0.42
ICPUESDA
1.00

Does It Work?

• Is a Huffman encoding optimal?

  • Is the locally optimal choice globally optimal?

  • Are the intermediate Huffman trees optimal?

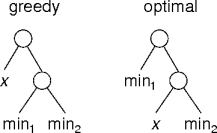
Local and Global Optimality

With repect to greedy: f(min1) ≤ f(x) l(x) ≤ l(min1)

• Greedy encoding size: f(min₁)l(min₁) + f(x)l(x)

• Optimal encoding size: f(min₁)l(x) + f(x)l(min₁).

• Greedy encoding size ≤ optimal encoding size.

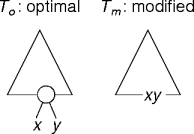
Optimal Subproblems

f(xy) = f(x) + f(y). Is Tm optimal? Yes: we're done.

• No. Find an T_mo, an optimal version of T_m.

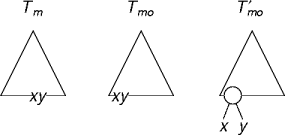
  T'mo is better than the optimal To, a contradiction.

School Consolidation

• A county C has n towns; each town has a school.

• Pick a subset S of towns such that:

  • Only towns in S have a school.

  • Every town in C is no more than 30 miles from a school.

  • S is minimal.

• For Monmouth County, n ≈ 210.

Exhaustive Solution

• Generate every possible subset of towns.

• For each subset:

  • Check the 30 mile constraint.

  • Check the size.

• This is an exponential algorithm.

  • For Monmouth County, 2²¹⁰ ≈ 1.6 × 10⁶⁶.

A Greedy Solution

set consolidate-simple(towns)

  schools = { }

  for t in towns
    if not covered(t, schools)
      schools ∪= { t }

  return schools

• There is no ordering; the greedy choice is random.

Does It Work?

• Not really.

  

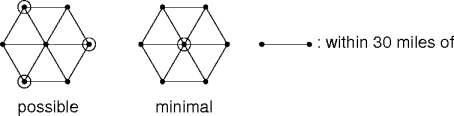
• The locally optimal choice is optimal by chance.

Another Greedy Solution

• Be greedy about coverage: pick popular towns.

  set consolidate-uncovered(towns)
  
    schools = { }
  
    for towns uncovered
      t = unpicked town with largest number
          of uncovered neighbors
      schools ∪= { t }
  
    return schools
  

Does It Work?

• Yes!

  

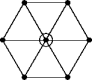
• Wait... what?

  

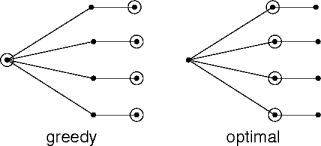
Yet Another Greedy Solution

• Similar to consolidate-simple(), but pick any road connecting two uncovered towns.

  set consolidate-paired(towns)
  
    schools = { }
  
    for towns uncovered
      r = a road connecting uncovered 
          t1 and t2
      schools ∪= { t1, t2 }
  
    return schools
  

Degrees of Failure

• Three greedy algorithms for consolidation (actually vertex cover), none of them work.

• How badly do they fail?

  • That is, how far away from optmial can their solutions be?

• consolidation-simple() and consolidation-uncovered() solutions are at most O(log n) away from optimal.

• consolidation-pair() solutions are at most 2 away from optimal.

Limiting Failure

• Non-optimal solutions may be close enough to optimal.

• Non-optimal algorithms may not go too far astray.

• If an algorithm is non-optimal, figure out how far astray it could go.

  • Or let somebody else figure it out.

Heuristics

• Non-optimal greedy solutions may be improved with heuristics.

  • Post-process solutions for local improvements.

  • Run greedy algorithm variants.

Post-Processing

• Solution post-processing is the same as it was for exhaustive search.

  • Local analysis for local improvements.

• For greedy CD filling:

  • Replace listed files with larger pairs of unlisted files.

Variant Contests

• Greedy algorithms are easy to make and fast to run.

  • Create several of them, run them all, take the best solution.

  • And then post-process the solution.

• For greedy CD filling:

  • Pick largest to smallest, smallest to largest, alternating smallest and largest.

References

• Greedy Algorithms, Chapter 17 in Introduction to Algorithms by Thomas Cormen, Charles Leiserson, and Ronald Rivest, MIT Press, 1999.

• Greedy Algorithms, Chapter 5 in Algorithms by Sanjoy Dasgupta, Christos Papadimitriou, and Umesh Vizirani, McGraw-Hill, 2008

This page last modified on 26 October 2008.