Divide and Conquer: CS 306 Lecture notes

Computer Algorithms II Lecture Notes

2 December 2008 • Divide and Conquer

Outline

Using Dividing
What Division Does
Divide and Conquer
Analysis
Recursion
Mergesort

Looking For x

unsigned ls-find(a[], n, x)

  for i = 1 to n
    if a[i] = x
      return i

  return 0

ls-find() does O(n) comparisons.

Quickly Looking For x

unsigned bs-find(a[], n, x)
  l = 0
  r = n + 1
  while l < r
    m = (l + r)/2
    if a[m] = x
      return m
    if a[m] < x
      l = m + 1
    else
      r = m
  return 0

bs-find() does O(log n) comparisons.

Comparison

Why is bs-find() faster than ls-find()?
bs-find() does two things ls-find() doesn't:
1. Divide the array in half.
2. Throw half the array away.
Which of these is more important?
- Dividing is cheap.
- Throwing away is expensive (requires ordered data).

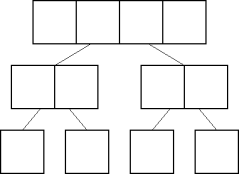
Dividing Find

unsigned d-find(a[], l, r, x)
  if l + 1 = r
    return a[l] = x ? l : 0
  m = (l + r)/2
  i = d-find(a, l, m, x)
  return i == 0 ? d-find(a, m, r, x) : i

dividing non-sorted find

There's not enough information to do better.
The correct subsolution is the ultimate solution.

Finding Min and Max

min-max(a[], n)

  min = max = a[1]
  for i = 2 to n
    if min > a[i]
      min = a[i]
    else if max < a[i]
      max = a[i]

  return min, max

min-max() uses 2(n - 1) comparisons.
Can it be done with fewer comparisons?

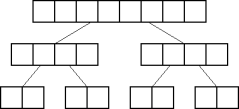
Using Dividing

min-max(a[], l, r)

  if l + 2 = r
    if a[l] < a[l + 1]
      return a[l], a[l + 1]
    else
      return a[l + 1], a[l]

  m = (l + r)/2
  mn1, mx1 = min-max(a, l, m)
  mn2, mx2 = min-max(a, m, r)

  return mn1 < mn2 ? mn1 : mn2,
         mx1 < mx2 ? mx2 : mx1

divided min-max

min-max() uses 3/2n + 1 comparisons.

What Division Does

Division produces subproblems; each subproblem produces subsolutions.
Subsolutions provide the information that can be exploited for efficiency.
- The smallest subsolutions are also usually trivial to solve.
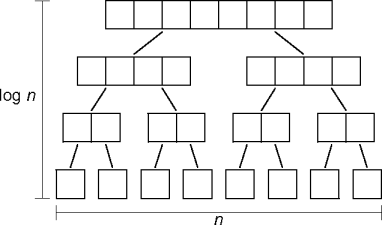
Division also limits the subproblems to log quantities.
- Good division does, anyway.

Divide and Conquer

The divide and conquer algorithm design technique:
1. Repeatedly divide each problem into smaller subproblems.
2. Solve the trivial subproblems.
3. Repeatedly combine subsolutions into larger solutions.
Divide and conquer is also the basis for other algorithm design techniques.

Analysis

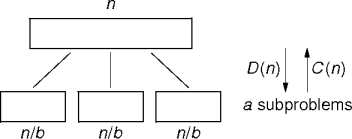
the masters theorem

Let T(n) be the cost of a divide-and-conquer solution on a problem of size n. Then

T(n) = aT(n/b) + D(n) + C(n)

or S if n is small enough.

Recursion

Divide and conquer is a stylized form of recursion.
General recursion allows arbitrary forms of subdivision.
Divide and conquer does too, but works best when the subdivision is uniform.

find(a[], n, x) m = n/2 if a[m] = x return true if a[m] < x return find(a + m, m, x) return find(a, m, x)

find(a[], n, x) if n = 0 return false if a[0] = x return true return find(a[1..n-1], n - 1, x)

Dividing to Sort

a data segment

Given a data segment,

a data segment

divide it into halves.

Now recurse on the two halves.
- When do you stop?

Reuniting Divisions

A segment of size less than two is sorted.
Two sorted subsegments can be merged back into the original segment.
- And the original segment will be sorted too.

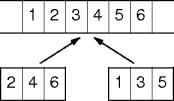
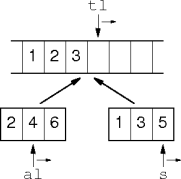
Merging

Scan from left to right, copying the minimum value.

merge(T * 
   tl, tr, al, am, ar)
 T * s = am
 while tl < tr
  if (al < am) ∧
     (s == ar or *al < *s)
   *tl++ = *al++
  else
   *tl++ = *s++

Mergesort

mergesort(T * aleft, aright, tleft, tright)

  len = aright - aleft

  if len > 1
    mid = len/2
    T * amid = aleft + mid
    T * tmid = tleft + mid

    mergesort(aleft, amid, tleft, tmid)
    mergesort(amid, aright, tmid, tright)
    merge(
      tleft, tright, aleft, amid, aright)

Analysis

mergesort analysis

In this case a = b = 2, D(n) = 1, C(n) = n, and S = 1.
Total work is O(n log n).

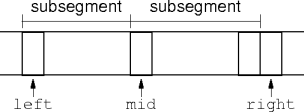
Array Merging

a data segment

The orignal data segment

a data segment

is split in place into halves.

a data segment

The subsegments occupy the segment they're supposed to merge into.

Array Mergesort

Declare a second array to merge into, then copy back to the original array.

mergesort(a[], n)
  copy = new [n]
  mergesort(a, a + n, copy, copy + n)
  for i = 1 to n
    a[i] = copy[i]
  delete [] copy

mergesort() on arrays takes O(n) space.

Linked-List Dividing

Linked lists can be divided with O(n) work if the list size is known.
- Walk over n/2 elements to the middle.
What if the list size isn't known?
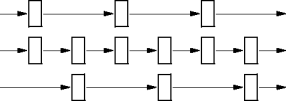
- Unzip the original list into two sublists with O(n) work.

Summary

Divide and conquer is an algorithm design technique.
- It's also a technique to add to other designs.
Divide and conquer is a stylized form of recursion.
Even division into subproblems provides the best opportunity for good performance.
Mergesort is a guaranteed O(n log n) sort.

References

Divide-and-conquer algorithms, Chapter 2 in Introduction to Algorithms by Sanjoy Dasgupta, Christos Papadimitriou, and Umesh Vazirani, McGraw-Hill, 2006.

Credits

All Hail Caesar by jpeepz under an AT-NC CC license.

T(n)	=	aT(n/b) + D(n) + C(n)
	or	S if n is small enough.