Computer Algorithms II Lecture Notes
4 December 2008 • Divide and Conquer in Practice
Outline
- Finding closest points.
The Closest-Pair Problem
- Given a set S of plainer points

Find the point pair with the smallest distance between them.
- Euclidian distance: sqrt((x1-x2)2+(y1-y2)2).
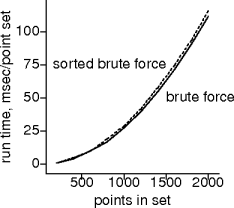
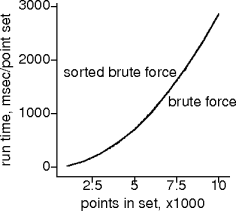
Dum and Fast
closest-pair(pts[], n)
p1 = 0
p2 = 1
d = dist(pts[p1], dst[p2])
for i = 0 to n - 1
for j = i + 1 to n - 1
if (dist(pts[i], pts[j]) < d)
d = dist(pts[i], pts[j])
p1 = i
p2 = j
return p1, p2
- Fast to implement, anyway.
Doing Better
- Can we do better?
- Asymptotically better, we hope.
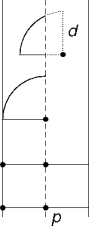
- Why consider points further than dmin away along the x axis?
- Sorting should help us, right?
Another Algorithm
closest-pair(pts[], n)
sort-by-x(pts)
p1 = 0
p2 = 1
d = dist(pts[p1], dst[p2])
for i = 0; i < n; i++
j = i + 1
while j < n ∧ pts[j].x - pts[i].x < d
if d > dist(pts[i], pts[j])
p1 = i
p2 = j
d = dist(pts[i], pts[j])
j++
return p1, p2
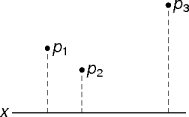
Does It?
- Apparently not.
- Sorting costs aren’t covered by pruning savings.
|
|
|
Dividing and Conquering
- Divide the point set into equal (more or less) halves.
- Stop dividing when the set has less than three points.
- At which point the solution is trivial.
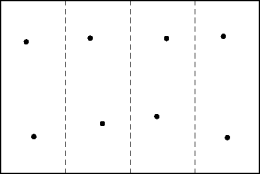
- Stop dividing when the set has less than three points.
Combining Subsolutions
- A subsolution is the closest point pair in the subproblem.
- Given two subproblems from a common parent,
- The parent’s solution is the smaller of the two child subsolutions.

Analysis
- Subdividing requires sorting the points by x (or y) coordinate, O(n log n).
- There are O(n) trivial subproblems.
- Each trivial subproblem is solved in constant time.
- Sibling subsolutions are combined in constant time.
- The sorting costs dominate for an O(n log n) solution.
Correctness
- The correctness argument is easy:
the divide and conquer solution to the closest point pair problem is wrong.
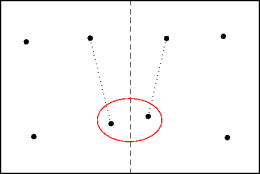
- The smallest point pair may straddle sibling subproblems.
- Subsolutions have to be combined more carefully.
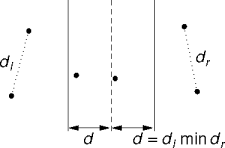
The Problem
- A true closest pair could be hiding in a strip around the subproblem dividing line.
- Combining sibling subsolutions requires another closest-pair search through all points within the minimum distance of the dividing line.
|
|
|
Expensive Solutions
- Exhaustively search the strip points.
- Apply divide and conquer to the strip points’ y coordinates.
- These solutions are complicated, and asymptotoically more expensive than O(n log n).
- What information’s being left on the table?
Bounded Search
- Points no closer to p than d can be ignored.
- This assumes ordered y coordinates.
- But didn’t this fail already? Do we know anything more now to make this solution possible?
|
|
|
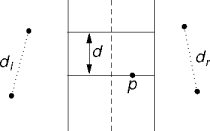
A Stricter Bound
- A strip point has at most two nearest neighbors on the other side.
- One’s enough, though.
- There are at most three candidate nearest neighbors on the other
side.
- Points within d of p's y value.
- A linear scan of M ≤ N strip points with a small bounded number of comparisons for each point.
|
|
|
Algorithm
closest-pair(pts)
if pts.size > 2
sort pts by x
l, r = divide(x)
d = min(closest-pair(l),
closest-pair(r))
strip = within-strip(d, x)
sort strip by y
for each p in strip
adjust d w.r.t. p
return d
Analysis
sort pts by x : O(n log n) l, r = divide(x) : odr(n) d = min(closest-pair(l), : T(n/2) closest-pair(r)) : T(n/2) strip = within-strip(d, x) : O(n) sort strip by y : O(n log n) for each p in strip : O(n) adjust d w.r.t. p : O(1)
- T(n) = 2T(n/2) + O(n log n), T(2) = 1.
- By the master theorm, T(n) = O(n log2 n).
Cheaper Sorting
- Sorting strip points by y is too expensive. Can it be cheaper?
- Divide and conquer!
- Two points can be sorted by y in constant time.
- Two point lists ordered by y can be merged into a point list ordered by y in linear time.
- Sorting by x can be done once at the beginning and charged to the whole algorithm.
Re-analysis
closest-pair(pts)
if pts.size > 2)
l, r = divide-on-x(pts) : odr(n)
dl, ptsl = closest-pair(l), : T(n/2)
dr, ptsr = closest-pair(r), : T(n/2)
pts = merge-on-y(ptsl, ptsr) : O(n)
d = min(dl, dr) : O(1)
strip = within-strip(d, pts) : O(n)
for each p in strip : O(n)
adjust d w.r.t. p : O(1)
return d, pts
- T(n) = 2T(n/2) + O(n), T(2) = 1.
- By the master theorm, T(n) = O(n log n).
References
- The “All-Pairs Closest Points” Problem by William Mahoney in Dr. Dobb’s Journal, January, 2003.
- Closest Pair, Section 8.5 in Introduction to Algorithms by Udi Manber, Addison Wesley, 1989.