Computer Algorithms II Lecture Notes

11 September 2008 • Asymptotic Analysis

Outline

• Characterizing algorithms and programs.

  • Measuring and estimating.

• Asymptotic estimates.

  • A behavior hierarchy.

  • Structural analysis.

• Examples

An Algorithm

• Algorithm 1.

  string read
  
  while getline(cin, str)
    read += str
  
  for i = 0 to read.size()
    if read[i] == '<'
      // process tag
  

Another Algorithm

• Algorithm 2.

  string read
  
  while getline(cin, str)
    read += str
    for i = 0 to read.size()
      if read[i] == '<'
        // process tag
        read[i] = ' '
  

• Which algorithm is better?

  • And what does “better” mean?

Comparing Algorithms

• There are many algorithms, all different.

• Which algorithm can be judged suitable?

  • It depends on your criteria.

    • Memory use, speed, message count, ...

    • Testable, maintainable, reusable, ...

• Consentrate on stable, easily quantifible resource use.

Measuring Performance

• Wire up the algorithm and measure its resuorce use.

  • Measure execution time, storage use, and so on.

• Measurements give definitive answers.

• Measurements give comparative answers.

  • Smaller (or bigger) is better.

Measuring Problems

• Meaningful measurements are hard.

• Measurements are context dependent.

  • Determining context accurately is difficult.

• Comparing results is hard.

  • Contexts must match to be meaningful.

• But algorithms don’t execute; they’re not code.

  • It requires implementing the algorithm.

Estimated Performance

• If you don’t know, guess (or estimate).

  • Ignore the details, go for the big picture.

  • Estimating is simpler than measuring.

    • At a cost of being less representative.

• Skillful professionals estimate well.

  • Estimation is a skill to develop.

Estimation Advantages

• Estimation works for algorithms.

• Estimates are more comparable then are measurements.

  • The context is mostly ignored when estimating.

• Estimates are more durable than are measurements.

  • Not as closely tied to hardware or software technology.

Estimate What?

• If you can measure it, you can estimate it.

  • And maybe even if you can’t measure it.

• Start with execution time.

  • Performance is usually related to other criteria.

    • It takes time to use a resource.

• Make sure you understand what’s being estimated.

Modeling Estimates

• A problem of a particular size causes an algorithm to use a particular amount of resource.

• Model a resource estimate as a function f(n).

• The algorithm is reduced to a function, other details abstracted away.

• Make sure you understand what the input and output represent.

Functional Model

• Model resuorce use as a function f(n).

• f(n) is the estimated resource for an input of size n.

  • What can n represent?

    • Whatever’s important: bits, lines, records.

  • What can f(n) represent?

    • Whatever’s important: behavior in time or space, messages, errors, dollars.

Sorting Example

• The function f(n) models resources used by a sorting algorithm.

• n is the number of elements being sorted.

  • Alternative: n is the number of bits being sorted.

• f(n) is the time it takes to sort n elements.

  • Alternative: f(n) is the number of comparisons made to sort n elements.

Database Example

• The function f(n) models the resources used by a distributed-database consensus algorithm.

• n is the number of machines over which the database is distributed.

  • Alternative: n is the percentage machines not responding.

• f(n) is the number of messages it takes to reach reach consensus.

Estimate Comparisons

• Algorithm A₁ has resource-estimate model f₁.

  Algorithm A₂ has resource-estimate model f₂.

  Now what? How do f₁ and f₂ compare?

• Given two functions, how do you compare them?

  • Point-by-point comparison (n = 1, 2, ...) isn’t too convenient.

Bounding Functions

• After modeling an algorithm by f(n), estimate f(n)’s behavior.

  • There are many ways to estimate f(n)’s behavior.

• An upper bound on f(n)’s behavior is useful.

  • It represents potential worst-case behavior.

  • Other bounds are possible, but harder to find.

Upper-Bounds

• An upper bound of f(n)’s behavior is a function g(n) with the property that
  C*g(n) ≥ f(n)
  as n grows without bound for some positive constant C.

  • In other words f(n) is never larger than g(n).

  • It’s an asymptotic estimate because n grows without bound.

Big-Oh Notation

• An alternative representation for f(n)’s upper bound is O(f).

  • That is, g(n) = O(f).

    “The function g is bounded above by the function f.”

  • The actual interpretation of “g(n) = O(f)” is strange.

• Sometimes also known as worst-case estimates.

Known Estimates

• After a while, the same estimates come up again and again.

  • The estimates also tend to be familiar functions.

• These estimates form a set of well-known signposts.

• The set of well-known estimates serve as a yardstick for comparing estimates.

Constant Behavior

• This is input-independent behavior

  • This is the ideal behavior.

  • But watch out for the value of C.

Logarithmic Behavior

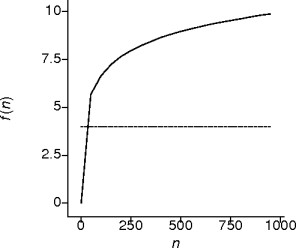
• This is repeated dividing behavior.

  • Binary search.

Linear Behavior

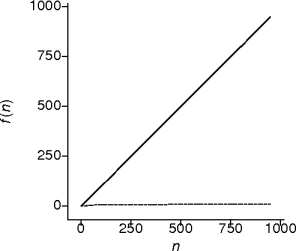
• This is touch every element behavior.

Log-Linear Behavior

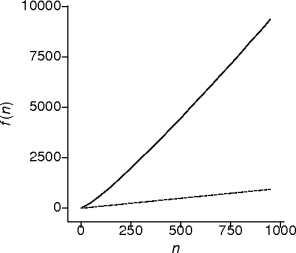
• This is sorting behavior.

• Repeatedly divide for every element.

Quadratic Behavior

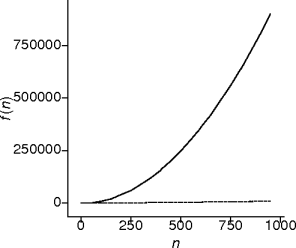
• This is double loop behavior.

Exponential Behavior

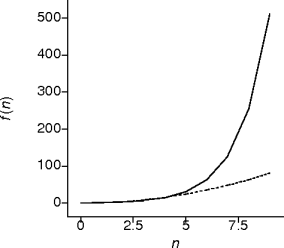
• This is systematic guessing behavior.

Factorial Behavior

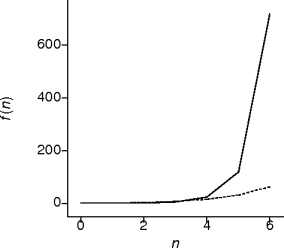
• This is permutation generating behavior.

A Behavior Hierarchy

Constant		O(1), hash table searching
Log		O(log n), binary search
Linear		O(n), linear search
Log-linear		O(n log n), heapsort
Quadratic		O(n2), bubble sort
Exponential		O(2n), subsetting
Factorial		O(n!), optimal route finding

• Higher is better.

  • A given value of n produces smaller numbers.

A Family Portrait

• Let n = 100.

  f	f(n)
  C	C
  log n	4.6
  n	100
  n log n	460.5
  n2	10,000
  n3	1,000,000
  2n	1,267,650,600,228,229 × 1015
  n!	93,326,215,443,944,152 × 1046

Comments

• Except for small n, improving asymptotic behavior is important.

  • Don’t fiddle with the code, fiddle with the algorithm.

  • Move down to the next lowest level of asymptotic behavior.

• When n is small, practically any algorithm will do.

Asymptotic Estimate Properties

• For any f(n), f(n) = O(f).

• O(f) + O(g) is O(max(f, g)).

  • Larger estimates swallow up smaller estimates.

  • max(f, g) may not exist as n grows without bound.

• O(f)*O(g) = O(fg).

  • The product of estimates is the estimate of the product.

Producing Estimates

• Given an algorithm how do you produce an estimate?

  • After you've decided on the input and output meanings.

• There are several techniques for producing estimates from algorithms.

  • Usually used in combination.

• Structural analysis is a simple and straightforward technique.

Structural Analysis

• Algorithms have a regular structure.

  • Statements, sequences, loops, and choice.

• Use program structure to derive asymptotic estimates.

  • Assign behavior to smaller units.

  • Combine units following algorithm structure to find behavior of larger units.

  • Repeat until the whole algorithm’s been combined into a single estimate.

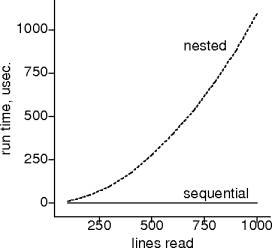
Running Example

• A running example: bubble sort.

    i = 0
    while i < n
      j = i + 1
      while j < n
        if a[i] > a[j]
  	std::swap(a[i], a[j])
        j++
      i++
    

Statements

• Usually O(1), but know your data structures.

  • Compare vec.size() with lst.size().

• Estimate the simple statements.

  i = 0 while i < n j = i + 1 while j < n if a[i] > a[h] swap(a[i], a[j]) j++ i++

  O(1) while i < n O(1) while j < n if a[i] > a[h] O(1) O(1) O(1)

if Statement

• if b s1 else s2

• Execute either s₁ or s₂, but which one?

  • Because we’re overestimating, use the larger of the estimates.

• Don’t forget b’s cost.

  • O(f_b) + O(max(f₁, f₂))

if Example

• Estimate the if statements.

  O(1) while i < n O(1) while j < n if a[i] > a[h] O(1) O(1) O(1)

  O(1) while i < n O(1) while j < n O(1) + O(1) = O(1) O(1) O(1)

Statement Sequence

• s₁ ; s₂

• s₁ is O(f), s₂ is O(g), so s₁; s₂ is O(f) + O(g)

• What is O(f) + O(g)?

  • Treat O(f) as a set of functions, pick a representative function and apply the definition of big-oh.

  • Take the larger of the two.

    • O(f) + O(g) is O(max(f, g))

Sequence Example

• Estimate the statement sequences.

  O(1) while i < n O(1) while j < n O(1) O(1) O(1)

  O(1) while i < n O(1) while j < n O(1) + O(1) = O(max(1, 1)) = O(1) O(1)

Loops

• while b do s

• s has asymptotic estimate O(f).

• s gets executed some number of times.

  • Asymptotically bound the number of times as O(g).

• The estimate is O(f)*O(g).

  • O(f)*O(g) is equivalent to O(f*g)

Loop Overhead

• The loop itself does constant work per iteration.

  • Ignore it.

  • This includes the cost of evaluating b.

• An implicit, and occasionally troublesome, assumption.

Loop Example

• Estimate the loops.

  O(1) while i < n O(1) while j < n O(1) O(1)

  O(1) while i < n O(1) O(n)*(O(1) + O(1)) = O(n) O(1)

To Finish.

• Estimate the statement sequence.

  O(1) while i < n O(1) O(n) O(1)

  O(1) while i < n O(1) + O(n) + O(1) = O(n)

• Estimate the loop

  O(1) while i < n O(n)

  O(1) O(n)*O(n) = O(n2)

To Finish..

• Estimate the statement sequence.

  O(1)
  O(n2)
  

• Done: O(n²).

• The structure of the algorithm determines the next step.

Subroutines

• Non-recursive subroutines are treated like a statement.

  • Guess at or know the estimate for a call.

• Recursive calls are tougher.

  • Solved with recurrence relations.

  • Among other things.

Be Wary

• Always treat estimates with suspicion.

• Pay attention to the constants, and to the assumptions made.

  • In particular, what's the input and output (resource) assumptions?

Constants

• Keep an eye on the constants.

  • Asymptotically identical algorithms may be (usually are) different.

  • For small n, constants are more important - linear search is usually good enough.

• Small estimates with large constants may be worse than a large estimate with a small constant.

Input and Output

• Estimate the right things.

  • What’s important: an expensive algorithm, or the number of times it’s called?

• Look at the right inputs.

  • Focus on what’s driving the algorithm.

  • Worrying about execution time on communication-bound computations.

Remember This?

string read

while getline(cin, str)
  read += str

for i = 0 to read.size()
  if read[i] == '<'
    // process tag

• Read in a string, then process all tags.

And This?

string read

while getline(cin, str)
  read += str
  for i = 0 to read.size()
    if read[i] == '<'
      // process tag
      read[i] = ' '

• Likewise: read in a string, then process all tags.

• Which program is better?

Let's Estimate!

while getline(cin, str)
  read += str

for i = 0 to read.size()
  if read[i] == '<'
    // process tag

• What’s the input?

  • It could be lines or characters processed.

• What’s the output?

  • How about statements executed.

Basic Statements

• Take input to be lines processed.

  • Assume n lines were read.

while getline(cin, str) : O(1)
  read += str : O(1)

for i = 0 to read.size() : O(1)
  if read[i] == '<' : O(1)
    // process tag : O(1)

Compound Statements

while O(1) : O(n)
  O(1)

for O(1)
  if O(1) : O(1)
    O(1)

• The while loop iterates O(n) times, executing O(1) + O(1) = O(1) statements on each iteration.

• The if statement executes O(1) + O(1) = O(1) statements.

Iteration Statements

O(n)

for O(1) : O(1)
  O(1)

• The for loop iterates O(n) times.

  • O(1) characters per line * O(n) lines.

Statement Sequences

O(n)

O(n)

• O(n) + O(n) = max(O(n), O(n)) = O(n).

• The number of statements executed is proportional to the number of lines read.

Second Program

• Reduce the basic statements.

while getline(cin, str) : O(1)
  read += str : O(1)
  for i = 0 to read.size() : O(1)
    if read[i] == '<' : O(1)
      // process tag : O(1)
      read[i] = ' ' : O(1)

Compound Statements

• The for loop iterates in proportion to the number of lines read.

Finishing Up

• O(n)*O(n) = O(n*n) = O(n²).

• O(n) vs. O(n²): the first program wins!

Does It?

• Apparently

• See the code.

Points to Remember

• Develop algorithms not programs.

  • Code programs from algorithms.

• Use performance criteria to select algorithms.

  • Keep in mind other criteria.

• Use asymptotic estimates for performance.

  • Remember these are estimates.

• Estimate performance using structural analysis.

  • Let the algorithm give you the next step.

• Understand what the estimates are saying.

  • Which algorithm is the better performer?