See Nyhoff, page 766.
The answers, in no particular order and approximately verbatim:
- The difference between a merge sort and a natural merge sort is that in a natural merge sort you chose your value based on a search of your data set, but in a regular merge sort you find the median to sort the data.
- A merge sort and a natural merge sort takes the data an divides it in halves. After this each half is then sorted and merged back together.
- A natural mergesort is when you break up components where they current exist. Mergesort brakes the group into two parts and then merges the two parts into one. Natural mergesort so as each box before merging them back.
- Mergesort uses a partition, while natural mergesort does not.
-
Mergesort divides the data into smaller blocks of data then it goes through the data from left to right comparing each value to one another determining which value is less than the other. After this is done it inserts the value into the array in order.
Natural mergesort is
- A natural mergesort is an external sort that combines two files while a mergesort operates on numbers in main memory.
- When comparing, mergesort can be considered an external sort whereas natural mergesort is not.
- Mergesort takes in outside data and implements this data into another sorted array in array-based sorting by calling the partition method after the outside sources have been input. A natural mergesort will still act as the same mergesort, except that natural mergesort seamlessly integrates with the rest of the already sorted array with no need for outside function calls. This is [?] will lower implementation times.
- I remember reading this section but am drawing a complete blank on what a mergesort did. Not starting off too strongly …
- A mergesort is slower, the algorithm is different. Natural mergesort also merges the partitioned pieces differently.
- Standard mergesort forces the two arrays into sorted order and merges them into one array. Natural mergesort takes two already sorted arrays and merges them into one array. If put into the correct situation, natural mergesort is much more efficient.
Not much. Using a binary search to locate x in the sorted part of the array uses O(log n) comparisons as opposed to O(n) in the unmodified insertion sort and so should be faster. However, once located, it's still necessary to shove the sorted elements to the right one, which takes O(n) work in either case.
The answers, in no particular order and approximately verbatim:
- The modified insertion sort would have O(n log n) time because the searching would take O(log n) times and the sorting would depend on the number of elements so it would be O(n)*O(log n) = O(n log n).
- A binary search uses n2 operations to search through an array to look for the next lowest # to be inserted into the array then it shifts the data after the inserter down one. This actually makes it take longer because it constantly needs to go through every element in order to find the next element to insert.
- If the insertion sort was improved by using a binary search, I would think there is a bit more improvement expected because the binary search will allow insertion sort to find the value that the inserted value should be placed beside faster.
- You should see a marginal increase in efficiency. A binary search looks through specified data to find the bitwise representation of the search field. Insertion sort already finds the next value greater than the pivot, so the increase would be minute.
- That actually would improve insertion sorts a decent bit, since by searching for specific binaries, you already will likely know where to put them. (If that's wrong, the answer is 42.)
- Since insertion sort is heavily dependent on assigning values rather than comparing them, implementing a better search would not have much of an affect on performance. A way to cut down on assignment overhead would be a more worthy endeavor.
- Binary search will improve the speed of the insertion sort to a degree based on what kind of data is attempting to be sorted and the amount of data. For a element that is 4-bit binary, the binary search will improve the timing of the insertion sort. But if the element off the array for example, is long long, which would be 8-bit, will slow down the sort and increase its implementation time by O(n2).
- Insertion sort is of the order O(n log n). By adding a binary search, I think the process is going a further additional order and thus I can't see any improvement to the unmodified version over the modified version.
-
Probably, a binary search is faster than an insertion sort. it breaks the values up to search, which is similar to a quicksort and quicksort is asymptotically faster than an insertion.
An insertion sort is O(n2) behavior and is just slightly better than a bubble sort.
- With a sort data access depends on the work If more work is put into improving the sort, the less work there will be to accessing data. Since the sort is being implemented with a binary search, some improvement should be expected because as the amount of work to improve the sort is increased, the amount of work to access the data is decreased.
-
A linear would “touch” every value at least n times and then another n times for the comparison which leaves us with O(n2).
A binary search would improve this quite a bit. Binary search would improve to O(½n2) because you must touch half of the elements twice, once to look at it and once for your comparison.
The sort doesn't. Sorting from the least- to most-significant digits moves adjacent values to separate piles and may never reunite them. For example, the standard (left-to-right) radix-exchange sort would group 101 and 103 in the same pile (the 100s pile), while the right-to-left sort would put them in separate piles (the 1s and 3s piles) where it is likely they will never be brought into proximity again.
The answers, in no particular order and approximately verbatim:
-
In a radix-exchange sort if the numbers are sorted from right to left then it
creates a sort that is descending.
- If the numbers are sorted from left to right, in a radix-exchange sort, the binary numbers would not be sorted.
- The sorted numbers are moving from the max value to the min value in the array. This places them in descending order from left to right.
- The sort would be sorted backwards. Then again, I am not sure. If it's binaries we're discussing, then it would have different outcomes.
- The compare condition for the exchange must be changed, i.e., a value that was greater than the radix would have been exchanged to the right in left to right sorting, whereas it would be shifted to the left in right-to-left sorting.
- The radix exchange sort is doing O(nb) amount of work. If the ordering is switched from left to right to right to left, the timing of the sort will increase naturally. Therefore when the sort is implemented, it will work in a worse case O(nb) scenario.
- There should be not much of a difference other than the elements in the array would be operated from the bottom up.
- A radix-exchange sort sorts left to right b/c left is the most important digit to sort by. If is right to left it will sort them but not necessarily going to be correct for every digit, left-most will be correct.
- A radix-exchange sort sorts binary numbers from left to right if it is being sorted from lowest to highest. If the data is being sorted from right to left it would be in descending order.
- If we use radix exchange sort to sort from right to left the decimal numbers will not be sorted in ascending or descending order. Using radix sort (from right to left) will sort the binary representations into a pattern, but when those numbers are converted back to ints then will not be in order.
- Instead of starting from the most significant digit you would be sorting from the least significant digit. The numbers are sorted in a descending list and not an ascending list.
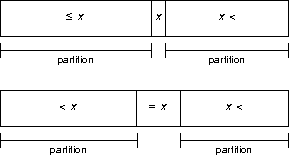
It should group equivalently-valued array elements with the pivot and split the array at the ends of the block. This would (may, because duplicate pivot values are not guaranteed) reduce the number of times the quicksort algorithm recurses over the array halves because the halves are smaller.
Alternatively, grouping the values equal to the pivot at the pivot places them in the array at their final locations in the sort, and there's no need to consider them further.
The answers, in no particular order and approximately verbatim:
- During a quicksort partition if the array element equals the pivot, then the pivot needs to be inserted to the left of the pivot and the partition should continue.
- If your pivot value equals an array element, you may have to make your pivot point = pivot point + 1 so the pivot point picked has a spot in the sort and is not left out of the end result of the sorted array.
- If there is such a condition where the array element equaled the pivot, then further partitioning may be avoided and just do the rest of the section from that final partitioning. This element is the ‘extra work’ to do sorting if such a condition was not met.
- The quicksort partition method works off of the basis that the partition will split every array into equal halves and does not take into account even or invalid partition events. If the partition method comes in contact with an element of the array that is equal to it's pivot point, ti is powerless. To handle this exception, the partition method should reconceive [?] the similar elements, at the element in the array that equal to the pivot point as the pivot point, voiding out the original so the similar elements are eliminated, then continue with the partition.
- When a quicksort partition comes across a value equal to the pivot, I would think it would move the value directly next to the pivot, on whichever side the partition has been made.
- Well, if it's @ the least-amount hand(?) pivot, then put it as lowest integer/value, if it's at highest, put in last, if it is middle, insert it next to the middle pivot. By grouping it with other pivots in a specified order, you run zero risk of missorting. Doing no action would run the risk of an error, depending on who programmed the quicksort partition function (if its nonstandard/modified).
- It should not take any special action because it is already handled in the partition function with ref[a[i]] ≤ pivot l++ where a[i] is the element in the array and l is the left element moving up the array.
-
If you are designing a data structure from scratch, you could have a counter for each data element, and increment the counter every time you find a duplicate value.
This solves the problem, but leaves you with more overhead and memory usage.
Alternatively, once you realize that you need to place a number in the region to the left or right of the pivot, you could add additional comparisons to make sure that the value that is there already is not a duplicate. If it is, you simply move to the next space and check for a duplicate value again. You continue this until you find a space that is not a duplicate.
- Partitioning shouldn't take any special action. The pivot is created so that this element of list does not have to move. If the pivot equals the array element, that element is used as the pivot and to the left are the elements of the array before the pivot and to the right are elements of the array that are after the pivot.
- The quicksort should check every value it's using against the pivot point. Then, the program should force the value into the slot before or after the pivot (whichever the programmer chooses). Otherwise, the program could crash when comparing 2 like terms and nothing to handle that scenario with.
- If there is a value in the array that equals the pivot, I think partitioning should simply place that value in the segment to the left of the pivot. If it is included in the segment, it will still be included in the sort and placed in the sorted array.