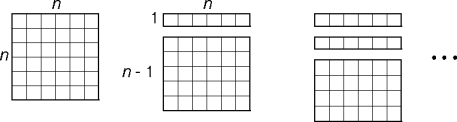
- This decomposition is degenerate.
for row = 1 to n
for col = 1 to n
s[row, col] =
a[row, col] + b[row, col]
row-by-row(row, n)
if row < n
col-by-col(row, 0, n)
row-by-row(row + 1, n)
col-by-col(row, col, n)
if col < n
s[row, col] =
a[row, col] + b[row + col]
col-by-col(row, col + 1, n)
row-by-row(0, n)

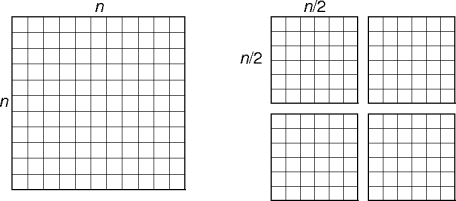
matrix-sum(a[], b[], x, y, n)
if n = 1
s[x, y] = a[x, y] + b[x, y]
else
n' = n/2
matrix-sum(x, y, n')
matrix-sum(x + n', y, n')
matrix-sum(x, y + n', n')
matrix-sum(x + n', y + n', n')
row-by-row and col-by-col or
matrix-sum?
row-by-row and col-by-col is complex but potentially as
efficient as the nested-loop code.
matrix-sum is less complex but unlikely to be as efficient.
matrix-sum loses. Why?
| C++, sec/sum | ||
|---|---|---|
| Method | -O0 | -O3 |
| loop | 0.71 | 0.27 |
| 2-recursive | 0.66 | 0.24 |
| 1-recursive | 1.50 | 1.10 |
Recursion
- Creates a bunch of subproblems.
- Solves each of the subproblems.
int f() int i, j double x // whatever
|
|
|
|
|
|
|
row-by-row(row, n)
if row < n
col-by-col(row, 0, n) // not a tail call
row-by-row(row + 1, n) // a tail call
col-by-col(row, col, n)
if col < n
s[row, col] =
a[row, col] + b[row + col]
col-by-col(row, col + 1, n)
col-by-col can be tail-call optimized into a loop.
for col = 0 to n - 1
s[row, col] =
a[row, col] + b[row + col]
row-by-row(row, n)
if row < n
col-by-col(row, 0, n)
row-by-row(row + 1, n)
col-by-col with the loop
row-by-row(row, n)
if row < n
for col = 0 to n - 1
s[row, col] =
a[row, col] + b[row + col]
row-by-row(row + 1, n)
row-by-row(row, n)
if row < n
for col = 0 to n - 1
s[row, col] =
a[row, col] + b[row + col]
row-by-row(row + 1, n)
row-by-row.
for row = 0 to n - 1
for col = 0 to n - 1
s[row, col] =
a[row, col] + b[row + col]
matrix-sum().
row-by-row() and col-by-col() with matrix-sum().
rprint(link)
if link ≠ nil
rprint(link→next)
print(link→data)
rprint'(link)
for l = link; l ≠ nil; l = l→next
stack.push(l)
while not stack.empty()
print stack.pop()→data