Computer Algorithms II Lecture Notes

9 October 2007 • Maximum Colinear Points

S is a set of integer points on a grid.

Lines through S may intersect points in S.

Find a largest subset of S through which a line can pass.

A point in S is either in a largest subset or not.

A point not in the subset can be ignored.

A point in the subset has a line passing through it. But which line?

Look at all lines through P.

For each line, count the other points it passes through.

Find the largest number of points intersected by any line through p.

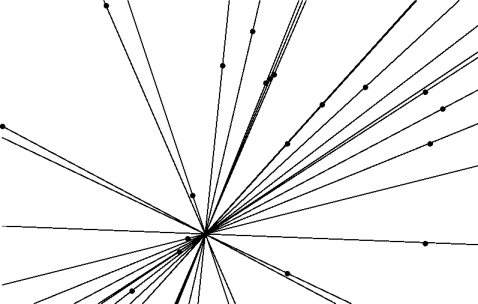
unsigned max-intersects(p, S)
  mx = 0
  for p2 in S
    if p ≠ p2
      mx = max(mx, intersects(p, p2, S))
  return mx

unsigned intersects(p, p2, S)
  cnt = 0
  for p3 in S
    if colinear(p1, p2, p3)
      cnt++
  return cnt

Three points are colinear if any two pair have the same slope.

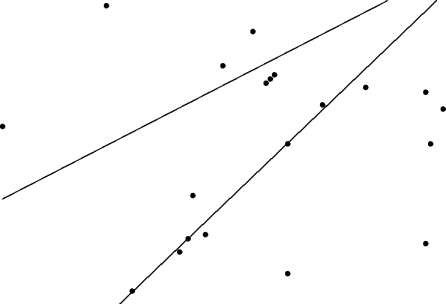
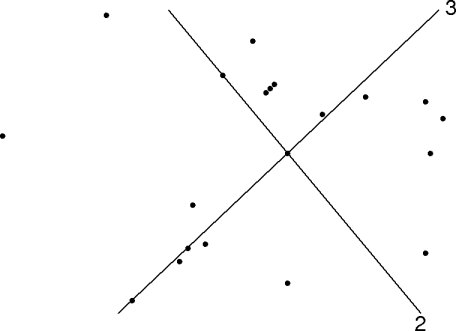
max-intersects() doesn't return the answer if p isn't in a subset.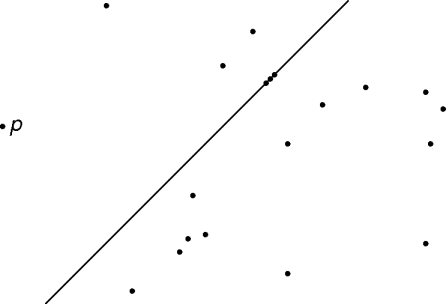

Run max-intersects() over every point in S.

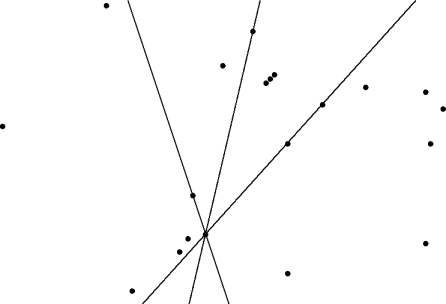
unsigned max-intersects(S)

  mx = 0

  for each p in S
    mx = max(mx, max-intersects(p, S)

  return mx

All points colinear with p have the same slope.

Find all slopes with p; the most frequent one is the answer.

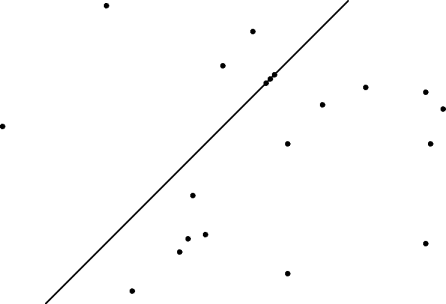
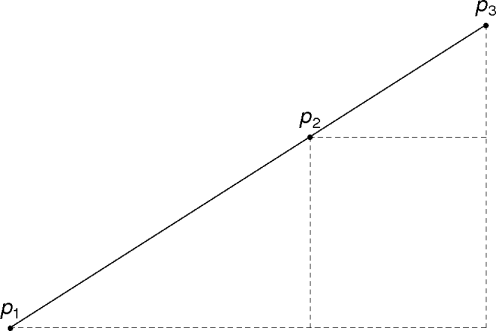
unsigned max_intersects(p, S)
  slopes = get-slopes(p, S)
  sort(slopes)
  return max-group-size(slopes)

A slope is a relatively-prime pair of numbers.

slope [] get-slopes(p, S)
  for p2 in S
    if p ≠ p2
      delta-x = p.x - p2.x
      delta-y = p.y - p2.y
      g = gcd(delta-x, delta-y)
      slopes.append(
        (delta-x/g, delta-y/g))

  return slopes

Order slopes as a fraction, or lexicographically.

bool < (slope s1, slope s2)
  return s1.x*s2.y < s1.y*s2.x

bool < (slope s1, slope s2)
  return 
    s1.x < s2.x ∨
    s1.x = s2.x ∧ s1.y < s2.y

Once grouped, find the most frequently occurring slope.

unsigned max-group-size(slopes)

  mx = 0
  n = slopes.size
  i = 0

  while i < n - mx
    while i + mx < n ∧
          slopes[i] = slopes[i + mx]
      mx++
    i++

  return mx

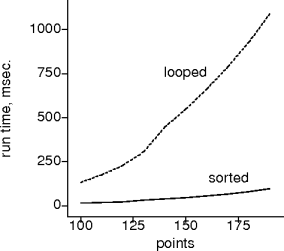
intersects() is O(n); max_intersects() is O(n²).

unsigned max-intersects(p, S)
  mx = 0
  for p2 in S
    if p ≠ p2
      mx = max(mx, intersects(p, p2, S))
  return mx

unsigned intersects(p, p2, S)
  cnt = 0
  for p3 in S
    if colinear(p1, p2, p3)
      cnt++
  return cnt

max-intersects() is O(n³).

unsigned max-intersects(S)

  mx = 0

  for each p in S
    mx = max(mx, max-intersects(p, S)

  return mx

get-slopes() is O(n).

slope [] get-slopes(p, S)
  for p2 in S
    if p ≠ p2
      delta-x = p.x - p2.x
      delta-y = p.y - p2.y
      g = gcd(delta-x, delta-y)
      slopes.append(
        (delta-x/g, delta-y/g))

  return slopes

max-group-size() is O(n).

unsigned max-group-size(slopes)

  mx = 0
  n = slopes.size
  i = 0

  while i < n - mx
    while i + mx < n ∧
          slopes[i] = slopes[i + mx]
      mx++
    i++

  return mx

max-intersects() is O(n log n).

unsigned max-intersects(p, S)
  slopes = get-slopes(p, S)
  sort(slopes)
  return max-group-size(slopes)

unsigned max-intersects(p, S)
  O(n)
  O(n log n)
  O(n)

max-intersects() is O(n² log n).

unsigned max-intersects(S)

  mx = 0

  for each p in S
    mx = max(mx, max-intersects(p, S)

  return mx

So What?

Summary

• Find a maximum colinear subset in a point set.

• Dumb solution: look at all lines.

  • An O(n³) solution.

• Slightly less dumb solution: look at all slopes.

  • An O(n² log n) solution.

• Slighlty less dumb wins.