Computer Algorithms II Lecture Notes

16 October 2007 • Exhaustive Search

Outline

• Exhaustive search.

• Exponential bounds and intractability.

• Pallatives.

• Intractable problems.

Some Files

$ du -sh *
170K    dj_Mitzura_-_If_you_really_want_to_rock_the_funky_beats.jpg
140M    dj_Mitzura_-_If_you_really_want_to_rock_the_funky_beats.mp3
74M     djspooky_ghostworldmix.m4a
8.0K    djspooky_ghostworldmix.txt
245M    fast-flux.mp3
2.0K    fast-flux.txt
109M    Green_Cheese_-_Green_Cheese_Vol_39_Reality_Adjustment.mp3
4.0K    Green_Cheese_-_Green_Cheese_Vol_39_Reality_Adjustment.txt
333M    Kper_-_Attention_Deficit_Disorder.mp3
6.0K    Kper_-_Attention_Deficit_Disorder.txt
336K    Tea_Time_at_Brian_Enos_House.jpg
110M    Tea_Time_at_Brian_Enos_House.mp3
4.0K    Tea_Time_at_Brian_Enos_House.txt

$ du -h
1.0G   .

$

A Problem

• Store as many files as possible on a CD with 700 MB available.

  • “As possible” means “with minimal unused space.”

• Do this every two weeks or so.

  • That is, automate it.

• How?

Some Solutions

• How about adding files from largest to smallest?

  • That doesn't work too well for files of size 351, 350, and 350 Mbytes.

• Ok, then how about adding files from smallest to largest?

  • That doesn't work too well either for files of size 1, 350, and 350 Mbytes.

• Ok, then how about...

Non-Solutions

• Any particular solution for packing files loses to a cleaver counter-example.

  • Maybe; nobody's sure.

• That leaves trying all solutions and keeping the best one found.

  • If a problem has a universal counter-example, then it doesn't have a solution.

  • Example: pack a 701 Mbyte file.

Example

• Given files of size 351, 350, and 350 Mbytes,

  files
  packed		sum
  0	=	0
  351	=	351
  350	=	350
  350	=	350
  351 350	=	701
  351 350	=	701
  350 350	=	700
  351 350 350	=	1051

Exhaustive Search

• The algorithm that tries every possible solution is known as exhaustive search.

  • Also known as brute force or the British Museum algorithm.

answer solve(p)
  candidates = generate-all-candidates(p)

  for each candidate in candidates
    if solution(p, candidate)
      return candidate

  return none

Example

files file-pack(files)

  candidates = possible-packings(file)
  max = 0
  solution = nil

  for each c in candidates
    if c.size < 700 and c.size > max
      solution = c
      max = c.size

  return solution

Applicability

• Exhaustive search has two requirements:

  1. Be able to generate all candidate solutions.

  2. Be able to check a candidate solution.

• Also, generating and checking candidates should be efficient.

  • Checking usually is, generating usually isn't.

Advantages

• Exhaustive search is an attractive algorithm-design technique:

  • It's widely applicable.

    • Particularly to search-oriented problems.

  • It's simple.

  • It's obviously correct, given correct generation and checking.

Disadvantages

• The principle disadvange to exhaustive search is the cost of generating candiates solutions.

• In particular, the number of candidate solutions is the problem.

  • It's impractical to use exhaustive search on problems of any size.

Example

• N files have how many candiate packings?

  • Each candidate is a subset of the n files.

  • An n-element set has many subsets?

• Let s be a subset of { f₁, f₂, ... f_n }.

  • Each file f_i is either in s or it isn't.

  • s = < 0, 1, ..., 0 >, an n-bit number.

  • There are 2ⁿ n-bit numbers.

Exponential Order

• A function with a Cⁿ upper bound has exponential order, O(2ⁿ).

  n		2n		GHz-1
  20		106
  30		109		1 sec.
  40		1012		16 min.
  50		1015		11 days

• Functions with exponential worst-case bounds are intractable.

Pallatives

• Exhaustive search works well for small values of n.

  • N less than 35 for file packing.

• Some problems may not have exponentially many candidate solutions.

  • There are only O(n²) lines through n planear points.

Remember This?

• The maximum path-sum problem.

  

• Given a number triangle, find a path with maximum sum.

The Algorithm

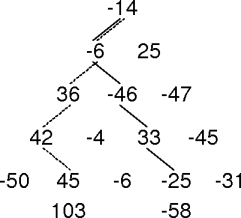
max-sum-path(triangle)

  all-paths = all-paths(triangle)
  max-path = pick(all-paths)
  max-sum = path-sum(triangle, max-path)

  for each path in all-paths
    sum = path-sum(triangle, path)
    if sum > max-sum
      max-sum = sum
      max-path = path

  return [ max-sum, max-path ]

Generating All Paths

• How do you generate all paths?

  

  • Each row requires a choice between two directions.

• This is a disguised subset problem.

Subset Generation

• Whenever a solution repeatedly pickts one of two choices, think “subsets”.

• Subsets of { f₁, f₂, ..., f_n }.

  • For each f_i, is f_i in the subset?

• Paths through a number triangle.

  • At each level, go left or go right?

• N binary choices is equivalent to a n-bit binary number.

Exhaustive Sorting

• How would you implement sorting using exhaustive search?

sort(a[])
  candidates = generate-all-candidates(a)

  for each candidate in candidates
    if sorted(candidate)
      return candidate

  return none

Generating Candiate Sorts

• What are the candiates solutions for sorting?

  • Various shufflings of the input array.

    Each suffling produces a different candiate. Each suffling is called a permutation.

• How many candidates are there?

  • n*(n - 1)*(n - 2) ... *2*1 = n!

Factorial Order

• How fast does n! grow? Is it O(2ⁿ)?

  • n! = n*(n - 1)*...*2*1

  • 2ⁿ = 2*2*...*2

• It seems that n! grows pretty fast.

  • Fast enough so that 2ⁿ is O(n!) with small constants (< 1).

• Great! Exhaustive searches can be bad (O(2ⁿ)) or really bad (O(n!)).

Route Planning

• Given a list of cities to vist, find a route that

  • Visits every city once,

  • ends where it started,

  • and is as cheap as possible for some cost.

  • Ignoring cost, such a route is called a Hamiltonian circuit.

    • And this problem is known as the travelling salesman problem.

Finding Routes

• Use exhaustive search to find a route.

  route file-route(cities)
  
    candidates = possible-routes(cities)
    solution = pick c in candidates
    min = c.size
  
    for each c in candidates
      if c.size < min 
        solution = c
        min = c.size
  
    return solution
  

Generating Routes

• How do you generate routes?

• Subject to road constraints, any list of the cities is a route.

  • The first and last cities are connected.

• That is, a route is a permutation of the city list.

  And there are O(n!) such routes.

Implementation Details

• The three most important details for exhaustive search are

  1. The algorithm outline.

  2. The candidate-generating code.

  3. The candidate-checking code.

• The candidate-checking code is closely related to the problem and usualy simple.

Algorithm Outline

• Exhaustive search problems have two flavors:

  1. Is there any solution for this problem?

  2. What is the best solution for this problem?

• The first flavor is called a decision problem.

  • Sorting, for example.

• The second flavor is an optimization problem.

  • CD packing or sum paths, for example.

Decision Problem Solutions

• Decision problems have straighforward exhaustive searches:

  answer solve(p)
    candidates = generate-all-candidates(p)
  
    for each candidate in candidates
      if solution(p, candidate)
        return candidate
  
    return none
  

Optimization Problem Solutions

• Optimization problems have slightly less straighforward exhaustive searches:

  answer solve(p)
  
    candidates = generate-all-candidates(p)
    best = pick a candidate
  
    for each candidate in candidates
      if candidate is better than best
        best = candidate
  
    return best
  

Generating Candidates

• Generating candidates usually involves one of three techniques:

  • Looping, as in maximum colinear points.

  • Subsets, as in CD packing.

  • Permutations, as in sorting.

• Candidate generation must be consistent and regular.

  • No duplicate candidates, no missed candidates.

Generating Subsets

• Subsets have already been identified with n-bit numbers.

  generate(problem)
    candidates = { }
    n = problem.size()
    for i = 0 to 2n - 1
      candidates.add(select(i, problem))
    return candidates
  

• select() makes subsets based on i's 1 bits.

Generating Permutations

• Permutations can be lexicographically ordered.

  generate(problem)
    candidates = { }
    p = first-permutation(problem)
    do candidates.add(p)
       p = next-permutation(p)
    while p ≠ first-permutation(problem)
    return candidates
  

• The STL implements permutation operations.

One Last Problem

• What's wrong with this code?

  answer solve(p)
    candidates = generate-all-candidates(p)
  
    for each candidate in candidates
      if solution(p, candidate)
        return candidate
  
    return none
  

Candidate Set Size

• The candidate set size could be enourmous (O(2ⁿ) or O(n!)).

• It is wasteful and dumb to

  generate all the candidates,
  store them, and
  evaluate them one by one.

  • Particularly when dealing with decision problems.

• How to fix?

A Revised Outline

• Generate each candidate and test it immediately.

  answer solve(p)
    solution = first-candidate()
  
    while candidates-left()
      candidate = next-candidate()
      if candidate better than solution
        solution = candidate
  
    return solution
  

A Revised Hierarchy

Constant		O(1)
Log		O(log n)
Linear		O(n)
Log-linear		O(n log n)
Polynomial		O(ni)
Exponential		O(2n)
Factorial		O(n!)

• Asymptotic values below the line represent intractable problems.

  • Resource growth outstrips availablility.

Intractable Problems

• Unfortunately,

  • Intractable problems are common, particularly optimization problems.

  • Many important problems are intractable.

    • Bin packing and Hamiltonian circuits, for example.

• More details in an algorithm complexity course.