Computer Algorithms II Lecture Notes

23 October 2007 • Assignment 2 Code Review

Outline

Problem and Solution Design.
Testing.
Coding comments.

The Problem

Sort three integer vectors to put all numbers of the same modulus in the same vector.
The sort should use the smallest possible number of between-vector moves.

The Answer

The answer requires only
- the modulus of the numbers in each vector and
- the total number of moves.

An Observation

There are only six possible sorts:

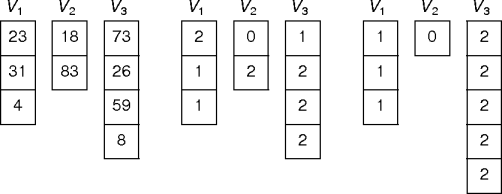
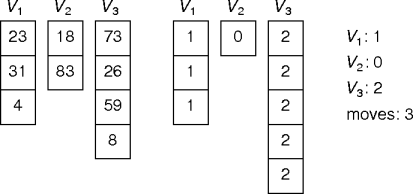
V₁: 0 0 1 1 2 2

V₂: 1 2 0 2 0 1

V₃: 2 1 2 0 1 0
Run through all the sorts and take the cheapest one.

A Partial Solution

sorts[][] = { { 0, 1, 2 }, { 0, 2, 1 }, 
              { 1, 0, 2 }, { 1, 2, 0 },
              { 2, 0, 1 }, { 2, 1, 0 } }

sort = 0
moves = sort(v1, v2, v3, sorts[sort])

for i = 1 to 5
  m = sort(v1, v2, v3, sorts[i])
  if m < moves
    moves = m
    sort = i

return sorts[sort], moves

More Observations

The vectors don't have to be sorted.
- Count the elements that would moved if the vectors were sorted.
A vector element moves at most once.
- Move it to the right vector and leave it there.
A vector element either moves or it doesn't.
- Keep track of one or the other; counting moves is easier.

Sorting

unsigned sort(v1[], v2[], v3[], order[])

  return moves(v1, order[0]) +
         moves(v2, order[1]) +
	 moves(v3, order[2])


unsigned moves(v[], mod)

  moves = 0

  for i = 1 to v.size() 
    if v[i] % 3 ≠ mod
      moves++

  return moves

Analysis

sort() is O(n), where n is the total number of vector elements,
- n = v1.size() + v2.size() + v3.size()
Checking all sorts is O(n).
The minimal sorting can be found with linear costs.

Testing

An exhaustive test set on small vectors.
- Is it right?
A random test set on large (≈ 10⁶) vectors.
- Is it fast?

Why Arrays Were Invented

int zeroMod1=0;
int oneMod1=0;
int twoMod1=0;
int zeroMod2=0;
int oneMod2=0;
int twoMod2=0;
int zeroMod3=0;
int oneMod3=0;
int twoMod3=0;

int sumAll=0;
int sumTotalCongruent=0;

int oneSum=0;
int twoSum=0;
int threeSum=0;
int fourSum=0;
int fiveSum=0;
int sixSum=0;

for (j = 0; j < one.size(); j++)
  if (one.at(j) % 3) == 0
    zeroMod1++
  else if (one.at(j) % 3) == 1
    oneMod1++
  else if (one.at(j) % 3) == 2
    twoMod1++

One alternative

unsigned mod1[3]

mod1[0] = mod1[1] = mod1[2] = 0

for (j = 0; j < one.size(); j++)
  mod1[one.at(j) % 3]++

This page last modified on 23 October 2007.
This work's CC license.