Computer Algorithms II Lecture Notes

18 September 2007 • Recursion Basics

Outline

• Some problems.

• Recursion

• Structural, inductive, and degerate recursion.

• Recursion use and abuse.

A Boxy Picture

• How do you draw this picture?

Breakfast Sequences

• An egg sandwich uses one egg, an omelette uses two eggs.

• Given n eggs, how many different breakfast sequences are there?

  • For example, if n = 3,

    S, S, S
    O, S
    S, O

  • There are three different sequences starting with three eggs.

Investments

• Every year you can invest in a stock, or
  every two years you can invest in a bond.

  • The same amount is invested every year.

  • One active investment at any time.

    

• The expected return in year y is S(y) for the stock and B(y) for the bond.

• Based on expected returns, what investment strategy maximizes return over n years?

Choices

• Given { 1, 2, 3, 4 } (n = 4), how many ways are there to choose 2 numbers?

  1, 2	2, 3	3, 4
  1, 3	2, 4
  1, 4

  • Six, apparently.

• Given n distinct items, how many ways are there to pick i ≤ n items?

Maximum Path Sum

• Given a number triangle, find a path with maximum sum.

  

Finding Max Sum Paths

• Find the neighbor triangles' max sum paths.

• Pick the neighbor with the larger max sum path.

Max Sum Path Code

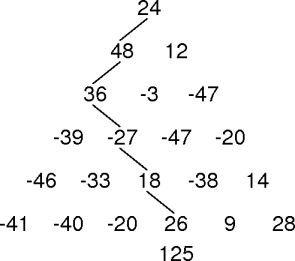
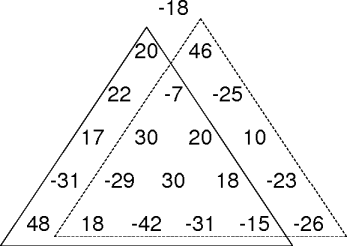
max-path-sum(t, row, col)
  if row == N
    return ( [ (row, col) ], t[row, col] )

  left-max-path = 
    max-path-sum(t, row + 1, col)
  right-max-path = 
    max-path-sum(t, row + 1, col + 1)

  if left-max-path[2] > right-max-path[2]
    return ( (row, col) ++ left-max-path[1],
             left-max-path[2] + t[row, col] )
  else
    return ( (row, col) ++ right-max-path[1],
             right-max-path[2] + t[row, col] )

Recursion

• General approach:

  1. Split a problem into smaller similar, subproblems.

  2. Repeat until the subproblems are trivial.

     • “Trivial” means solved with no computation.

  3. Recombine subproblem solutions into a solution for the originating (sub)problem.

• This approach is called recursion.

Recursion Format

• The trivial subcomputation in step 2 is called the base case.

• The recursive steps 1 and 3

  • Simplifies a problem into smaller similar subproblems.

  • Recursively applies the algorithm to the subproblems.

  • Combines the subproblem solutions into a more complete solution.

Recursion Advantages

• The advantages of exploiting recursion include:

  • Simplicity: the trivial problem, dividing problems and recombining solutions.

  • Wide applicability: recursion can be discovered in surprising places.

  • Transparency: correct recursive algorithms are correct (almost) by inspection.

  • Cliched: the same damn thing over and over.

Recursion Disadvantages

• Problems with recursion include

  • Computational expense.

    • Easily and (usually) automatically transformed into more efficient forms.

  • Opacity, particularly among the uninitiated.

    • Oh well.

  • Subtle design errors.

    • Few hiding places.

Finding Recursion

• Recursion relates directly to the problem's structure.

• There are three general recursion sources:

  1. The problem or data structure; structural recursion.

  2. Linear structures; inductive recursion, a special case of structural recursion.

  3. optimized (usually) semi-recursive algorithms; degenerate recursion.

Structural Recursion

• Structural recursion is (almost) a gimme; it follows from the problem or data structure.

  • Although the problem or data structure may not be the best one to use.

• Examples:

  • The max sum path problem: a triangle is an apex with left and right subtriangles.

  • Trees: a tree is a node with a set of trees as children.

Recursive Data Structures

• A recursive data structure D is defined by

  • A base case giving the simplest possible instance of D.

  • A constructive case that combines one or more D instances and other data into a new, single D instance.

• A recursive algorithm undoes the structure created by the constructive case.

  • And stops recursing at the base case.

Example

• An n-ary tree of type T is

  • Nothing (the base case).

  • A value of type T and up to n n-ary trees of type T.

  A recursive algorithm:

  bool find(v, root) if root == nil return false if root.value == v return true return find(v, root[0]) || ... find(v, root[n-1])

Inductive Recursion

• Inductive Recursion is structural recursion over linear structures.

  • Arrays, sequences, and the like.

• The subdivision is usually (but not always) into a single element and the rest of the structure.

• With care, inductive recursion can be automatically transformed into efficient looping code (tail-call optimization).

Example

• Find an element x in an array.

• Base case: finding an element in an empty array is trivial.

• Recursive case:

  • Splint an n-element array into a 1-element array and an array with n - 1 elements.

  • If x is in the 1-element array, return true.

  • Otherwise, return the result of recursing on the array with n - 1 elements.

Example Code

bool find(x, a[])
  if a.size == 0
    return false
  else 
    if a[0] == x
      return true;
    else
      return find(x, a[1..a.size()])

Breakfast Sequences

• An egg sandwich uses one egg, an omelette uses two eggs.

• Given n eggs, how many different breakfast sequences are there?

  • For example, if n = 3,

    S, S, S
    O, S
    S, O

  • There are three different sequences starting with three eggs.

Recursive Breakfasts

• Recurse over the cost of a breakfast sequence in eggs.

  • The breakfast sequence S, R costs one egg plus whatever the rest of the sequence R costs.

  • The breakfast sequence O, R costs two eggs plus whatever the rest of the sequence R costs.

  • The empty breakfast sequence costs nothing.

Breakfast Code

• Return the number of breakfast sequences that can be formed with n eggs.

  int seq-count(eggs)
  
    if eggs < 1
      return 0
  
    c = 1 + seq-count(eggs - 1)
    if eggs > 1
      c += 1 + seq-count(eggs - 2)
  
    return c
  

Degerate Recursion

• Sometimes extra information can be used to modify the recursive structure to produce a better design.

  • But possibly not producing something following the typical recursive pattern.

• Example: searching for x in an unordered array vs. an ordered array.

Unordered Array Searching

• No extra knowledge about an unordered array; use straight inductive recursion.

  bool find(x, a[])
    if a.size == 0
      return false
    n = a.size/2
    if a[n] == x
      return true
    return find(x, a[0..n - 1]) || 
           find(x, a[n + 1..a.size])
  

Ordered Array Searching

• The extra ordering information helps eliminate the subproblems.

  bool find(x, a[])
    if a.size == 0
      return false
    n = a.size/2
    if a[n] == x
      return true
    if a[n] < x
      return find(x, a[n + 1..a.size])
    else
      return find(x, a[0..n - 1])
  

Recursion Requirements

• To use recursion successfully, should have

  • A base case (a trivial subproblem).

  • A way to divide the problem into subproblems.

  • A way to combine subproblem solutions.

Recursive Design

• Make sure the base case is

  • Really a base case (that is, a trivial instance of the problem).

  • Is correctly solved.

• Make sure the recursive step

  • Creates subproblems related into the original problem.

  • Combines subproblem solutions into a solution for the larger problem.

Recursion Pitfalls

• Although it's simple, it's possible to get recursion wrong.

  • The base case is wrong, incomplete, or incorrectly solved.

  • The subproblems are incorrectly derived from the original problem.

  • Subproblem solutions are incorrectly combined into an invalid solution for the orignal problem.

Wrong Base Cases

• The base case for factorial is 0, not 1.

  int factorial(n)
    if n == 1
      return 1
    return n*factorial(n - 1)
  
  
  int factorial(n)
    if n == 0
      return 1
    return n*factorial(n - 1)
  

Incomplete Base Cases

• How many 3- and 5-cent stamps equal any amount over 7 cents?

  • For example, 11 cents equals one 5-cent and two 3-cent stamps.

• The recursion seems easy:

  • The base case is 8 = 3 + 5.

  • For any value n > 7, n = n' + 3.

  • One more 3-cent stamp than needed for n'.

Stamp Counting Code

• That seems easy enough; here's the code.

  int-pair stamps(n)
    if n == 8
      return (1, 1)
    return (1, 0) + stamps(n - 3)
  

• Unfortunately, this code is wrong. Why?

Revised Code

• There are three base cases:

  8 = one 3-cent stamp + one 5-cent stamp.
  9 = three 3-cent stamps + no 5-cent stamps.
  10 = no 3-cent stamps + two 5-cent stamps.

  int-pair stamps(n)
    if n == 8
      return (1, 1)
    if n == 9
      return (3, 0)
    if n == 10
      return (0, 2)
    return (1, 0) + stamps(n - 3)
  

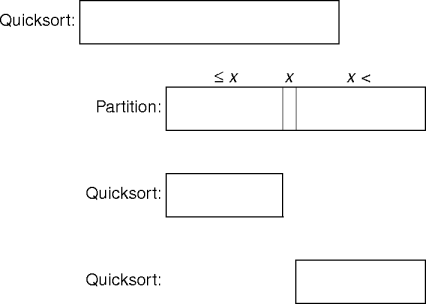
Bad Subdivisions

• The subproblems must be strictly smaller than the original problem.

  • If not, the recursion won't terminate.

• The subproblems must be really related to original problem.

  • Otherwise the subproblem solutions won't be related to the original problem's solution.

Quicksort

• Quicksort partitioning is slightly tricky code; getting it wrong breaks quicksort.

Improper Combinations

• Incorrectly combining correct subproblem solutions may lead to an incorrect original-problem solution.

• Given a set of planer points, find a pair with minimal distance between them.

  

Closest Points

• Repeatedly divide the point set in half until each piece contains at most two points.

  For two points, return the points; otherwise return nothing. From each half select the closest pair and return the smaller of the two pairs.

• Unfortunately, this doesn't work. Why?

Dividing Closest Points

• A closest pair of points may exist between divisions of the point set.

  

• Correctly recombining subproblem solutions requires more work than just comparing the subproblem solutions.