in-range(l, r) holds and in-range(l, m)
doesn't hold, then in-range(m + 1, r) holds.
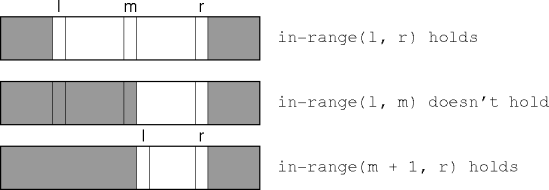
in-range(l, r)and not in-range(m, r)
means in-range(l,m - 1).
a and a value x, return
a[i] = x or
-1 if no such i exists.
aas array in an ascending order.The return value i if
a[i]=xThe return value
-1if no such i exists.The O(log n) limit on comparisons.
a must be in ascending order.
a isn't in ascending order?
in-range(). in-range(l, r)
means
Ifvis ina, it must be ina[l..r].
l = r, then either a[l] equals v or it doesn't.
l > r, then v isn't in the array.
l < r, then more work is needed.
l, r = 1, n
while true
// in-range(l, r)
if l = r
return a[l] = v ? l : -1
if l > r
return -1
if l < r
// do more work
l + 1tororltor - 1.
m = (l + r)/2.
m = (l + r)/2 help reduce the range?
m, examine a[m]. There are three cases:
1:a[m] > v
2:a[m] = v
3:a[m] < v
a[m] = v) holds, the search succeeded.
a[m] ≠ v help reduce the range?
a is sorted, v can't appear in one of the
subranges 0..m or m..n, but which one?
a is sorted in ascending order,
a[m] < v means in-range(l, m) doesn't hold,
a[m] > v means in-range(m, r) doesn't hold.
in-range(l, r) holds and in-range(l, m)
doesn't hold, then in-range(m + 1, r) holds.

in-range(l, r)and not in-range(m, r)
means in-range(l,m - 1).
int find(a[], n, v)
l, r = 0, n - 1
while true
// in-range(l, r)
if l > r
return -1
else
m = (l + r)/2
if a[m] = v, return m
if a[m] < v, l = m + 1
if a[m] > v, r = m - 1
in-range() is an example of an invariant.
r - l can be the value.
while true
if l > r
return -1
else
m = (l + r)/2
if a[m] = v, return m
if a[m] < v, r = m - 1
if a[m] > v, l = m + 1
l ≤ m < r.
l = m may not reduce the range.
l = m + 1 reduces the range.
find(start, end, x, size)
m = size/2
if a[m] < x
return find(start, m - 1, x, m)
if a[m] > x
return find(midpoint + 1, end, x, m)
if a[m] = x
return m
if size = 1
return -1
find(start, end, x, size)
m = size/2
// What's the interval?
if a[m] < x
return find(start, m - 1, x, m)
// The correct half-interval?
if a[m] > x
return find(m + 1, end, x, m)
// The correct half-interval?
if a[m] = x
return m
// How do you get here?
if size = 1
return -1
find(a, x)
first = 0
last = a.size()
i = last/2
while (a[i] ≠ x) or
(last ≠ i and first ≠ i)
if a[i] > x
last = i
else if a[i] < x
first = i
i = first + (last - first)/2
if a[i] = x
return x
return -1
while (a[i] ≠ x) or
(last ≠ i and first ≠ i)
// Is a[i] defined?
if a[i] > x
last = i
else if a[i] < x
first = i
i = first + (last - first)/2
// Is the interval smaller?
if a[i] = x
return x
return -1
find(a, first, last, key)
m = (first + last)/2
if m > last
return -1
if a[m] = key
return m
if a[m] > key
return find(a, m + 1, last, key)
return find(a, first, m - 1, key)
find(a, first, last, key)
m = (first + last)/2
if m > last
return -1
if a[m] = key
return m
if a[m] > key
return find(a, m + 1, last, key)
// The correct half interval?
return find(a, first, m - 1, key)
// The correct half interval?