Lecture Notes for Telecommunications

27 September 2004 - Noisy Channels

Noise and Information Theory

• Noise in information is a corruption of a signal across a communication channel.

  • Noise causes the destination to receive something different from what was sent by the source.

• Shannon's model is approximately

Noise

• Suppose a source sends a symbol A_s from the set S = { A₁, A₂, ..., A_m } and a destination receives a symbol A_R from S.

• Noise can be deterministic or random.

• Deterministic noise always changes A_s to a specific A_r.

  • A_s = A_r with no noise.

• Random noise changes A_s to an arbitrary other symbol A_n.

  • Because the message set is known to both sides, messages corrupted out of the set can be recognized and rejected.

Noise vs. Capacity

• What happens when we communicate over a noisy channel?

• Consider transmitting fair coin flips over a noisy channel.

  • The channel mutates 1 bit out of 100 on average.

• The receiver knows, on average, 90% of the messages are correct, but not which messages are the correct ones.

• What does noise do to the information content of the channel?

Entropy Under Error

• If the source has entropy H(s), what is the entropy at the receiver?

  • With no error it's the same.

  • If there is error, how much uncertainty does the medium add?

• H_s(r) is the entropy at the receiver when the source is message known.

• What is the entropy of the whole system H(s, r)?

  • With no noise, H(s, r) = H(s) = H(r).

  • With noise, H(s, r) = H(s) + H_s(r) = H(r) + H_r(s).

Noise and Capacity

• Noise adds extra uncertainty, which reduces the source's information content.

• The capacity of the channel is reduced by the uncertainty at the receiver.

  C = H(s) - H_r(s)

• The conditional entropy H_r(s) is called equivocation.

  • It measures the uncertainty about the symbol received.

Equivocation Example

• To continue the 1 per 100 noisy channel example.

• If the source sends H, the receiver gets a H with p = 0.99 and a T with p = 0.01.

• From the entropy definition

  Hr(s)	=	-0.99 log2 0.99 - 0.01 log2 0.01
  	=	0.81 bits/second

Equivocation and Correction

• The equivocation tells us how much information we have to put into the system to correct for medium errors.

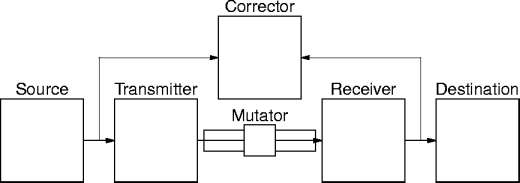
Equivocation and Communication

• Equivocation can be reduced via redundancy.

  • This reduces equivocation, it doesn't eliminate it.

• But doesn't redundancy eat up capacity?

  • No, not at the capacity defined previously.

A Discrete Channel with Noise

• Let a source have entropy H and a noisy channel have capacity C.

• If H <= C, then communication can occur with an arbitrarily small equivocation.

• If H > C, then communication can occur with arbitrarily small equivocation not less than H - C.

• In both cases the source has to be encoded to add extra data.

This page last modified on 14 November 2004.