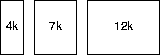
The queue of waiting jobs is
(The queue head's on the left; jobs exit the queue in strict queue order.) When the memory manager's done all waiting jobs are executing. Which of the four free-list allocation policies mentioned in class and in the text does the memory manager use? Explain.
Assuming the free list is stored in the left-to-right order given in the picture (10k, 4k, 18k), the behavior of the four free-list allocation policies are:
- First fit: The 4k process first fits in the 10k free block, leaving a
6k block of free space (free list: 6k, 4k, 18k).
The 7k process first fits in the 18k free block, leaving a 11k free block (free list: 6k, 4k, 11k).
The 12k process fits in none of the free blocks. The memory manager ends without having scheduled the final waiting process.
- Next fit: The 4k process first fits in the 10k free block, leaving a
6k block of free space (free list: 6k, 4k, 18k).
Starting from the 4k free block, the 7k process first fits in the 18k free block, leaving a 11k free block (free list: 6k, 4k, 11k).
Starting at the 6k free block, the 12k process fits in none of the free blocks. The memory manager ends without having scheduled the final waiting process.
- Best fit: The 4k process first fits exactly in the the 4k free block
(free list: 10k, 18k).
The 7k process first fits in the 10k free block with 3k overage and in the 18k free block with 11k overage; the 10k free block wins (free list: 3k, 18k).
The 12k free block fits in the 18k free block. The memory manager ends having scheduled the all waiting process.
- Worst fit: The 4k process fits in the 18k free block with maximum
overage 14k (free list: 10k, 4k 14k).
The 7k process first fits in the 14k free block with maximum 7k overage (free list: 10k, 4, 7k).
The 12k free block fits in none of the free blocks. The memory manager ends without having scheduled the final waiting process.
The memory manager apparently uses the best-fit allocation policy.
Most answers to this question were correct.
The job scheduler can slow down the flow of jobs into the system, which gives free space a chance to coalesce into larger blocks rather than being continually fragmented into smaller pieces.
Many answers to this question handed-off free-list management to the job scheduler under the assumption that the job scheduler knows more than the free-list manager does about prospective process sizes.
for i = 1 to 10
for j = 1 to 10
for k = 1 to 10
// non-big loop body
or to have a big loop body
for i = 1 to 10 // 300-line loop body
Explain.
Poor paging behavior results from excessive disk-IO, which depends on how many pages gets touched, not how many times a page gets touched. It's better for a loop to have a small loop body fitting in fewer pages than a larger one taking up more pages.
Many answers tried to argue that the overhead associated with a deeply nested loop could force bad paging performance, but translating the loops into the equivalent while loops shows that the loop code would be a small fraction of even a modest loop body.
The virtual-address space has n-digit virtual addresses ranging from 0 to 10n - 1; for example a 4-digit virtual-address space ranging from 0 to 9999 inclusive. The page size is 10s for 0 <= s <= n; there are 10n - s pages. The right-most s digits of a virtual address are the page offset; the left-most n - s digits are the page index.
Many answers made this question much harder than it was; a surprising number of answers tried to define a conversion between decimal and binary numbers.