When looking a solution to a problem, it's often helpful to look at simple
cases first. Given a photograph and a trace, if the trace has no points, then
the solution is easy: the trace doesn't appear in the photograph. Similarly,
if the trace has one point, then the trace appears n times, where n
is the number of bubbles in the photograph. Notice that the one-point trace
does require a transformation: the trace point has to be translated to the
bubble point. However, the one-point matching is obvious, and there's no need
to go through the transformation.
If the trace contains two points, then it matches each pair of bubbles in the
photorgraph; the trace apears n(n-1)/2 times. Because the trace and
photograph are both sets, the order of the matching doesn't matter. Given the
trace points t1 and t2 and the photograph bubbles b1 and
b2, the matching could be either (t1, b1) and (t2,
b2) or (t2, b1) and (t1, b2).
Like the one-point trace, the two-point trace needs transformations to have the
match go through. And like the one-point trace, the match is obvious and the
transformation itself isn't required. However, the two-point transformation is
not as simple as one-point transformation, and so it might be useful to take a
closer look just to make sure everything's jake.
Conceptually, but not technically, transforming trace points t1 and
t2 into the bubbles b1 and b2 requires three steps:
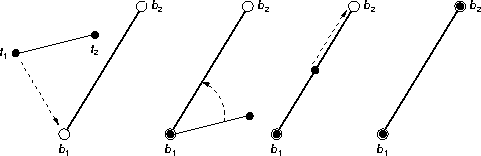
- Apply a translation to the trace points so that t1 co-incides
to bubble point b2 (because matching is unordered, the choice
of trace point and bubble is arbitrary).
- Rotate t2 about t1 so that t2 lies on the line
segment defined by (b1, b2).
- Scale t2 so it co-incides with b2.
The geometrically astute will have noticed that these steps aren't quite right:
Step 1 should translate the trace points so that t1 co-incides with the
origin, and there should be a Step 4 that translates the trace points so that
t1 co-incides with b1.
Now for three-point traces. Ignoring the third point for a second, the
remaining two trace points can be matched to any pair of bubbles. If the third
trace point, under the same transformations, matches a bubble, then the trace
matches. In any event, the search for matches continues with every possible
pair of bubble points.
There is one refinement needed by trace matching. Given the trace and
photograph
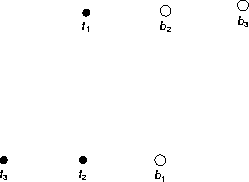
mapping t1 to b2 and t2 to b1 results in no match,
but mapping t2 to b2 and t1 to b1 produces a match.
Once a trace has more than two points, the order in which bubble pairs are
matched to trace is does matter, and both should be tried while searching for
matches.
Traces with more than three points are handled in the same way in which the
three-point traces were handled.
Before going on to the code, it might be useful to consider an alternative
analysis using simplification. Rather than simplify the trace, as was done
above, we could have simplified the photograph. If the trace contains n
points, then any photograph with less than n bubbles contains no traces.
If the photograph contains n bubbles, then it may or may not contain the
trace depending on the existance of an apropriate transformation, but what is
the transformation?
Aparently, simplifying the photograph isn't helpful. The valuable simple cases
- zero, one, two - are too trivial to tell us anything interesting and the
first non-trivial case can't help us find the transform we need. (Of course,
the real problem may be that we aren't clever enough to figure out if the
simple cases are telling us anything, or to figure out what the transform is.
This is why problem solving should be apporached from several directions; it
increases the chance that we'll be able to understand at least one of the
possible solutions.)
With all the machinery we're going to develop, main() is simple: read the
input, check it, look for tracks, and output any found.
<main()>=
int
main() {
bc_photograph photo;
bc_traces traces;
check_error(read_input(std::cin, photo, traces));
check_error(check(photo, traces));
std::for_each(traces.begin(), traces.end(),
track_finder(std::cout, photo));
}
Defines main (links are to index).
Used below.
The track-finder functor used by main() is a good example of
poorly-designed software. It's poorly designed because it tries to do too much
in one place: it tries to both find the tracks in the photograph and then print
them. It would be better to split out the finding and printing functions into
separate components, but I won't do that because I'm lazy - I mean, because
it's good to have some bad examples for you to contemplate, because you can try
your hand at designing and writing better software, and because I'll probably
work it through as an example during the code review.
<the track-finding-and-outputting functor>=
struct track_finder {
std::ostream & os;
const bc_photograph & photo;
// Create a new track finder with the given output stream and photograph.
track_finder(std::ostream & os, const bc_photograph & photo)
: os(os), photo(photo) { }
// Print the occurences of the given trace.
void operator () (const bc_trace & trace) {
track_list trks = find_tracks(photo, trace);
if (trks.empty())
os << trace.name << " does not occur in the photograph.\n";
else {
std::sort(trks.begin(), trks.end(), track_greater);
os << trace.name << " occurs " << trks.size()
<< " time" << (trks.size() == 1 ? "" : "s")
<< " in the photograph.\n";
std::copy(trks.begin(), trks.end(),
std::ostream_iterator<track>(os, "\n"));
}
}
};
Defines track_finder (links are to index).
Used below.
<main.cc>=
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <iterator>
#include <numeric>
#include <cassert>
#include "input.h"
#include "analysis.h"
#include "check.h"
// Deja vu c++ style.
static std::ostream & operator << (std::ostream &, const track &);
static std::ostream & operator << (std::ostream &, const triple &);
static unsigned size_add(unsigned, triple);
static bool track_greater(const track &, const track &);
<the track-finding-and-outputting functor>
static double
average_size(const track & trk) {
// Return the average size of the bubbles in the given track.
assert(not trk.empty());
return
static_cast<double>(std::accumulate(trk.begin(), trk.end(), 0, size_add))/
static_cast<double>(trk.size());
}
static void
check_error(const std::string & emsg) {
// If emsg contains an error, print it and die.
if (not emsg.empty()) {
std::cerr << "! " << emsg << ".\n";
exit(EXIT_FAILURE);
}
}
<main()>
static std::ostream &
operator << (std::ostream & os, const triple & t) {
// Write the given triple to the given output stream; return the output
// stream.
return os << t.x << " " << t.y;
}
std::ostream &
operator << (std::ostream & os, const track & trk) {
// Write the given track to the given output stream; return the output
// stream.
std::copy(trk.begin(), trk.end(),
std::ostream_iterator<triple>(std::cout, " "));
return os << "average bubble size " << average_size(trk);
}
static unsigned
size_add(unsigned s, triple t) {
// Return the sum of the given value and the size of the given triple.
return s + t.s;
}
static bool
track_greater(const track & t1, const track & t2) {
// Return true iff the average bubble size of t1 is larger than the average
// bubble size of t2.
return average_size(t1) > average_size(t2);
}
Defines average_size, check_error, main, main.cc, size_add, track_greater (links are to index).
This code is written to a file (or else not used).
<bc.h>=
#ifndef _bc_h_defined_
#define _bc_h_defined_
#include <vector>
#include <string>
struct ipair { int x, y; };
typedef std::vector<ipair> ipairs;
struct bc_trace {
std::string name;
ipairs trace;
};
typedef std::vector<bc_trace> bc_traces;
typedef bc_traces::const_iterator bct_citer;
struct triple {
int x, y;
unsigned s;
};
typedef std::vector<triple> bc_photograph;
typedef bc_photograph::iterator bcp_iter;
#endif
Defines bc.h, bc_photograph, bct_citer, bct_iter, bc_trace, bc_traces, ipair, triple (links are to index).
This code is written to a file (or else not used).
Input has a regular strucure: it's a bubble-chamber photograph followed by a
sequence of zero or more trace specs. A bubble-chamber photograph is a
sequence of zero or more triples. A trace spec is a trace name followed by a
sequence of zero or more pairs. All told, input comprises three sequences: of
triples (the photograph) the traces, and the pairs (the trace coordinates).
All those sequences suggests it might be handy to create a read function
generic on the type of data being read. We can go a step further and make the
read function generic on the container into which the items read will be
stored.
<input procedures>=
template < class Container >
static void
read_um(std::istream & is, Container & c) {
// Read a set of traces from the given input stream and store them in the
// given container. Return an empty string if everything went well;
// otherwise return an informative error message.
typedef std::istream_iterator<typename Container::value_type> is_iter;
c.clear();
std::copy(is_iter(is), is_iter(), std::back_inserter<Container>(c));
}
Defines read_um (links are to index).
Used below; next definition.
To make those istream-iterators work correctly, we're going to need to define
stream extractors for the three types of data that we're going to read. Start
with trace-coordinate pairs. It's leagl for the x coordinate to be missing,
but the y coordinate must be present if x is.
The extractor throws a domain-error exception if anything goes wrong. Thowing
an exception is better than the alternative (which is a global variable) and
the exception doesn't leave this file.
<input procedures>+=
static std::istream &
operator >> (std::istream & is, ipair & ip) {
// Read a pair from the given istream and store it in the given variable.
// Throw a domain-error exception containing an informative error message
// if anything goes wrong.
if (not (is >> ip.x))
return is;
if (not (is >> ip.y))
throw std::domain_error("Input error while reading trace y coordinate");
return is;
}
Used below; previous and next definitions.
Photo triples are similar to trace-coordinate pairs. It's leagl for the x
coordinate to be missing, but the other two parts of the triple (the y
coordinate and the bubble size) must be present, and the bubble size must be
positive, otherwise the input's invalid.
The variable s is necessary because the bubble size coordinate in the
triple is an unsigned, and a negative value would get turned into a positive
one (reading a negative value into an unsigned variable does not signal a read
error, probably to be consistent with the way C++ handles assginments of ints
to unsigneds).
<input procedures>+=
static std::istream &
operator >> (std::istream & is, triple & t) {
// Read a triple from the given istream and store it in the given variable.
// Throw a domain-error exception containing an informative error message
// if anything goes wrong.
if (not (is >> t.x))
return is;
if (not (is >> t.y))
throw
std::domain_error("Input error while reading photograph y coordinate");
int s;
if (not (is >> s))
throw
std::domain_error("Input error while reading photograph bubble size");
if (s < 1) {
std::ostringstream oss;
oss << "Non-positive bubble size " << s << " read from input";
throw std::domain_error(oss.str());
}
t.s = s;
return is;
}
Used below; previous and next definitions.
Reading a trace spec is just a little bit tricky. A trace is a name followed
by a sequence of pairs. The tricky part comes from determining why the pair
reading ended. If the pair reading ended because the eos or bad bit is set,
then that gets taken care of elsewhere. If pair reading bangs into the next
trace name, then the fail bit gets set set, and that has to be cleared to
enable reading the next trace. This approach isn't fool-proof, but then doing
fool-proof stream I-O is hard.
<input procedures>+=
std::istream &
operator >> (std::istream & is, bc_trace & bct) {
// Read a trace spec from the given istream and store it in the given
// variable. Throw a domain-error exception containing an informative error
// message if anything goes wrong.
if (is >> bct.name) {
read_um(is, bct.trace);
if (is.fail())
is.clear();
}
return is;
}
Defines read_um (links are to index).
Used below; previous and next definitions.
With all the preliminaries out of the way, reading the input becomes simple:
read the photograph, read the traces, and handle any errors that occur by
unwrapping the exception and returning the error message. The choice of the
exception type is arbitrary and probably not the best choice, but the issue
isn't that important because the exception doesn't propigate outside the code
in this file (but you have to read and understand all the code in this file to
make sure that the local-propigation claim is true).
Photo-triple reading can also end by banging into a trace name. In this case,
however, all error bits are unconditionally cleared because the fail bit should
be cleared, and the eof and bad bits will be set again on the next read.
<input procedures>+=
std::string
read_input(std::istream & is, bc_photograph & photo, bc_traces & traces) {
// Read a bubble-chamber photograph and a set of traces from the given input
// stream. Return an empty string if everything went well; otherwise return
// an informative error message.
try {
read_um(is, photo);
is.clear();
read_um(is, traces);
}
catch (std::domain_error & de) {
return de.what();
}
return "";
}
Defines read_input (links are to index).
Used below; previous definition.
And that's it for input.
<input.cc>=
#include <iterator>
#include <iostream>
#include <stdexcept>
#include <sstream>
#include "input.h"
// Deja vu c++ style.
template < class Container > void read_um(std::istream &, Container &);
<input procedures>
Defines input.cc (links are to index).
This code is written to a file (or else not used).
<input.h>=
#ifndef _input_h_defined_
#define _input_h_defined_
#include <istream>
#include <string>
#include "bc.h"
// Read a bubble-chamber photograph and a set of traces from the given input
// stream. Return an empty string if everything went well; otherwise return an
// informative error message.
extern std::string read_input(
std::istream &, bc_photograph &, bc_traces &);
#endif
Defines input.h (links are to index).
This code is written to a file (or else not used).
After the input checking done during input, there isn't much checking left to
do.
<input-checking procedures>=
std::string
check(bc_photograph & photo, bc_traces & traces) {
// Check the given photo and traces for errors; return a discriptive error
// message or nothing if there's no errors.
const std::string emsg = check_photo(photo);
return emsg.empty() ? check_traces(traces) : emsg;
}
Defines check (links are to index).
Used below; next definition.
The triple stream extractor has already checked for non-positive bubble sizes,
so the only error that could occur in a photo is bubbles with duplicate (x, y)
coordinates but different bubble sizes.
<input-checking procedures>+=
static std::string
check_photo(bc_photograph & photo) {
// Check the photo data; return an informative error message if something's
// wrong, otherwise return an empty string.
std::sort(photo.begin(), photo.end());
while (true) {
bcp_iter i = std::adjacent_find(photo.begin(), photo.end());
if (i == photo.end()) break;
const bcp_iter j = i++;
if (j->s != i->s) {
std::ostringstream oss;
oss << "Bubble at (" << j->x << ", " << j->y << ") has sizes "
<< j->s << " and " << i->s;
return oss.str();
}
}
return "";
}
Defines check_photo (links are to index).
Used below; previous and next definitions.
The std::sort() and std::adjacent_find() generic algorithm need
less-than and equality predicates (respectively) over triples that ignore the
bubble size. Here they are.
<input-checking procedures>+=
static bool
operator < (const triple & t1, const triple & t2) {
return (t1.x < t2.x) or ((t1.x == t2.x) and (t1.y < t2.y));
}
static bool
operator == (const triple & t1, const triple & t2) {
return (t1.x == t2.x) and (t1.y == t2.y);
}
Used below; previous and next definitions.
The only problem with traces is duplicate trace names.
<input-checking procedures>+=
static std::string
check_traces(bc_traces & traces) {
// Check the traces; return an informative error message if something's
// wrong, otherwise return an empty string.
std::sort(traces.begin(), traces.end());
const bct_citer i = std::adjacent_find(traces.begin(), traces.end());
if (i != traces.end()) {
std::ostringstream oss;
oss << "There are two or more traces named " << i->name;
return oss.str();
}
return "";
}
Defines check_traces (links are to index).
Used below; previous and next definitions.
Trace predicates are based entirely on trace names.
<input-checking procedures>+=
static bool
operator < (const bc_trace & t1, const bc_trace & t2) {
return t1.name < t2.name;
}
static bool
operator == (const bc_trace & t1, const bc_trace & t2) {
return t1.name == t2.name;
}
Used below; previous definition.
And that's it for input checking.
<check.cc>=
#include <algorithm>
#include <iostream>
#include <sstream>
#include "check.h"
// Deja vu, c++ style.
static std::string check_photo(bc_photograph &);
static std::string check_traces(bc_traces &);
static bool operator < (const triple &, const triple &);
static bool operator < (const bc_trace &, const bc_trace &);
static bool operator == (const triple &, const triple &);
static bool operator == (const bc_trace &, const bc_trace &);
<input-checking procedures>
Defines check.cc (links are to index).
This code is written to a file (or else not used).
<check.h>=
#ifndef _check_h_defined_
#define _check_h_defined_
#include <istream>
#include <string>
#include "bc.h"
// Read a bubble-chamber photograph and a set of traces from the given input
// stream. Return an empty string if everything went well; otherwise return an
// informative error message.
extern std::string check(bc_photograph &, bc_traces &);
#endif
Defines check.h (links are to index).
This code is written to a file (or else not used).
The input data is not in a particularly convenient form: bubble size isn't
needed to find traces in the photograph (but it is used to pick among several
tracks found, which is done elsewhere), the coordinates are in integers, but
should probably be doubles given the possibility of scaling and rotating
coordinates, and the points should be in a set rather than a vector.
This code preps the photo and trace data to make it more amenable for analysis
and then translates the data back again. Trace coordinates are transformed to
points, and the points are stored in a set, which takes care of duplicates in
the input data.
<conversion procedures>=
static point
ipair2point(const ipair & ip) {
// Convert the given ipair to a point; return the point.
return point(ip.x, ip.y);
}
static points
ipairs2points(const ipairs & ips) {
// Convert the given list of ipairs into a list of points; return the point
// list.
points pts;
std::transform(ips.begin(), ips.end(),
std::inserter(pts, pts.end()),
ipair2point);
return pts;
}
Defines ipair2point, ipairs2points (links are to index).
Used below; next definition.
Bubble coordinates are also translated into points and stored in a set. The
bubble size is ignored because it's not needed to find traces.
<conversion procedures>+=
static point
triple2point(const triple & tpl) {
// Convert the given triple to a point; return the point.
return point(tpl.x, tpl.y);
}
static points
triples2points(const triples & tpls) {
// Convert the given list of triples into a list of points; return the point
// list.
points pts;
std::transform(tpls.begin(), tpls.end(),
std::inserter(pts, pts.end()),
triple2point);
return pts;
}
Defines triple2point, triples2points (links are to index).
Used below; previous and next definitions.
The result of the analysis is a list of point sets, each point set representing
a trace found in the photograph. These point sets have to be translated back
into bubbles in the photograph.
<conversion procedures>+=
static track_list
pointslist2tracklist(const points_list & ptsl, const bc_photograph & photo) {
// Convert the given list of points into a list of tracks using triples taken
// from the given photograph; return the track list.
track_list trksl;
std::transform(ptsl.begin(), ptsl.end(),
std::inserter(trksl, trksl.end()),
std::bind1st(std::ptr_fun(points2track), photo));
return trksl;
}
Defines pointslist2tracklist (links are to index).
Used below; previous and next definitions.
A point set gets transformed into a trace track point by point, matching the
coordinate values.
<conversion procedures>+=
static track
points2track(const bc_photograph photograph, const points pts) {
// Convert the given point set to a track using triples taken from the given
// photograph; return the track;
track trk;
std::transform(pts.begin(), pts.end(),
std::inserter(trk, trk.end()),
std::bind1st(std::ptr_fun(point2triple), photograph));
return trk;
}
Defines points2track (links are to index).
Used below; previous and next definitions.
Given a point and a photograph, the point gets converted into the bubble
closest to the point.
<conversion procedures>+=
static triple
point2triple(const bc_photograph photograph, const point pt) {
// Convert the given point to a triple from the given photograph; such a
// triple is assumed to exist.
const bc_photograph::const_iterator tpl =
std::find_if(photograph.begin(), photograph.end(),
std::bind2nd(std::ptr_fun(tpl_eq_pt), pt));
assert(tpl != photograph.end());
return *tpl;
}
static bool
tpl_eq_pt(const triple tpl, const point pt) {
// Return true iff the given triple equals the given point.
return eq(tpl.x, pt.x) and eq(tpl.y, pt.y);
}
Defines point2triple, tpl_eq_pt (links are to index).
Used below; previous definition.
After all that prep work, the actual analysis is simple.
<analysis.cc>=
#include <algorithm>
#include <cassert>
#include <functional>
#include "analysis.h"
#include "tform.h"
typedef std::vector<triple> triples;
// Deja vu c++ style.
static points triples2points(const triples &);
static points ipairs2points(const ipairs &);
static track_list pointslist2tracklist(
const points_list &, const bc_photograph &);
static bool tpl_eq_pt(const triple, const point);
static track points2track(const bc_photograph, const points);
static triple point2triple(const bc_photograph, const point);
track_list
find_tracks(const bc_photograph & photograph, const bc_trace & particle) {
// From the given photograph extract a list of tracks matching the given
// particle trace; return the track list.
return pointslist2tracklist(
find_tracks(
triples2points(photograph),
ipairs2points(particle.trace)),
photograph);
}
<conversion procedures>
Defines analysis.cc, find_tracks, triples (links are to index).
This code is written to a file (or else not used).
<analysis.h>=
#ifndef _analysis_h_defined_
#define _analysis_h_defined_
#include "bc.h"
typedef std::vector<triple> track;
typedef std::vector<track> track_list;
// Return a list of tracks found for the given particle in the given photoraph.
extern track_list find_tracks(const bc_photograph &, const bc_trace &);
#endif
Defines analysis.h, track, track_list (links are to index).
This code is written to a file (or else not used).
As mentioned in the design section, the search for traces is transform based.
A transformation that maps two trace points into two photograph points is
applied to the rest of the trace points. The resulting set of transformed
trace points is compared against the photograph points, and if a match is found
for every transformed trace point, then the trace exists in the photograph.
<trace-search procedures>=
static void
find_track(
const point & p1, const point & p2, const points & photo,
const points & trace, points_list & tracks) {
// Try to map the given particle trace into a track in the given photrograph
// using the given points as reference; push any tracks found in the given
// track list.
points transformed_trace;
transform_points(p1, p2, trace, transformed_trace);
points common_points;
std::set_intersection(
photo.begin(), photo.end(),
transformed_trace.begin(), transformed_trace.end(),
std::inserter(common_points, common_points.end()));
if (common_points.size() == transformed_trace.size())
tracks.push_back(transformed_trace);
}
Defines find_track (links are to index).
Used below; next definition.
Searching a photograph for a trace involves comparing every pair of bubbles in
the photograph with the trace. This code contains the only explicit C++ looping
construct in the program, becasue I couldn't think of a simple and convenient
way to implement a double-indexed loop using generic algorithms.
<trace-search procedures>+=
points_list
find_tracks(const points & photo, const points & trace) {
// Return a list of all the tracks of the given trace found in the given
// photograph.
points_list tracks;
if (not trace.empty() and (trace.size() <= photo.size()))
if (trace.size() == 1)
std::transform(photo.begin(), photo.end(),
std::back_inserter<points_list>(tracks),
point2points);
else {
const points_citer e = photo.end();
for (points_citer i = photo.begin(); i != e; ++i) {
points_citer j = i;
while (++j != e) {
find_track(*i, *j, photo, trace, tracks);
find_track(*j, *i, photo, trace, tracks);
}
}
}
return tracks;
}
Defines find_tracks (links are to index).
Used below; previous and next definitions.
The point_transform functor derives a transformation and applies it to the
given trace points. The two important (and only public) methods in the functor
are the constructor that defines the transform mapping the trace line segment
(tp1, tp2) to the photograph line segment (pp1, pp2)
<transform-functor public member functions>=
point_transform(
const point & p1, const point & p2, const point & p3, const point & p4)
: p1(p1), p2(p3) {
scale = find_scale(p1, p2, p3, p4);
const double delta_a = find_delta_a(p1, p2, p3, p4);
cos_a = cos(delta_a);
sin_a = sin(delta_a);
}
Used below; next definition.
and the call-operator overload that applies the derived transformation to a
given trace point. Remember (from the Design Section) that the transformation
consists of a translation, followed by scale, followed by a rotation, followed
by a final translation.
<transform-functor public member functions>+=
point operator () (const point & pt) const {
point pt1, pt2;
pt1.x = (pt.x - p1.x)*scale;
pt1.y = (pt.y - p1.y)*scale;
pt2.x = cos_a*pt1.x - sin_a*pt1.y;
pt2.y = sin_a*pt1.x + cos_a*pt1.y;
pt2.x += p2.x;
pt2.y += p2.y;
return pt2;
}
Used below; previous definition.
The rest of the transform functor is generic geometry.
<the transform functor>=
struct point_transform {
<transform-functor public member functions>
private:
double distance(const point & p1, const point & p2) {
// Return the Euclidian distance between the given points.
const double
delta_x = p2.x - p1.x,
delta_y = p2.y - p1.y;
return sqrt(delta_x*delta_x + delta_y*delta_y);
}
double find_delta_a(
const point & p1, const point & p2, const point & p3, const point & p4) {
// Return the angular distance from the line (p1, p2) to the line (p3, p4).
const double
a1 = atan2(p1.y - p2.y, p1.x - p2.x),
a2 = atan2(p3.y - p4.y, p3.x - p4.x);
return a2 - a1;
}
double find_scale(
const point & p1, const point & p2, const point & p3, const point & p4) {
// Return the scale that makes the line (p1, p2) as long as the line (p3, p4).
const double d = distance(p1, p2);
assert(d > epsilon);
return distance(p3, p4)/d;
}
// The origin (first) point of the trace.
const point p1;
// The destination point in the photograph.
const point p2;
// The scale and rotation angles for the transformation.
double scale, cos_a, sin_a;
};
Defines distance, find_delta_a, find_scale, point_transform (links are to index).
Used below.
Once the point-transform functor's been defined, transforming a trace is a
matter of creating an apropriate instance of the functor and rubbing it over
the points in the trace.
<trace-search procedures>+=
static void
transform_points(
const point & p1, const point & p2,
const points & pt, points & transformed_pt) {
// Given the photograph points p1 and p2 and the particle trace pt, return
// the uniform transformation of pt such that pt's first point maps into p1
// and pt's last point maps into p2.
assert(pt.size() > 1);
std::transform(
pt.begin(), pt.end(),
std::inserter(transformed_pt, transformed_pt.end()),
point_transform(*pt.begin(), *--pt.end(), p1, p2));
}
Defines transform_points (links are to index).
Used below; previous definition.
And that's it for trace searching. The rest of the code is housekeeping.
<tform.cc>=
#include <algorithm>
#include <cmath>
#include <iterator>
#include <cassert>
#include "tform.h"
// What "close enough" means.
static const double epsilon = 0.001;
// Deja vu c++ style.
static void transform_points(
const point &, const point &, const points &, points &);
static points point2points(point);
<the transform functor>
<trace-search procedures>
bool
eq(double x1, double x2) {
// Return true iff x1 is close enough to x2 to be equal.
return fabs(x1 - x2) < epsilon;
}
bool
operator < (const point & p1, const point & p2) {
// Return true iff p1 is less than p2.
return
(p1.x - p2.x < -epsilon) or
(eq(p1.x, p2.x) and (p1.y - p2.y < -epsilon));
}
static points
point2points(point p) {
// Turn the given point into a singlton point set.
points ps;
ps.insert(p);
return ps;
}
#ifdef TESTING
// g++ -o test-tform -DTESTING -ansi -pedantic -Wall tform.cc && ./test-tform
#include <cstdlib>
#include <unistd.h>
#include <iostream>
static int rint(int n) { return (random() % n) - n/2; }
static std::ostream &
operator << (std::ostream & os, const point & p) {
// Write the given point to the output stream os; return os.
return os << p.x << " " << p.y;
}
static void doit(
const point & p1, const point & p2, const point & p3, const point & p4) {
points trace, otrace;
otrace.insert(p1);
otrace.insert(p2);
trace.insert(p3);
trace.insert(p4);
points transformed_trace;
transform_points(p1, p2, trace, transformed_trace);
if (otrace != transformed_trace) {
std::copy(trace.begin(), trace.end(),
std::ostream_iterator<point>(std::cout, ", "));
std::cout << "\n";
std::copy(transformed_trace.begin(),
transformed_trace.end(),
std::ostream_iterator<point>(std::cout, ", "));
std::cout << "\n";
std::cout << p1 << ", " << p2 << "\n";
}
}
static void perm_test(
const point & p1, const point & p2, const point & p3, const point & p4) {
std::vector<point> points;
points.push_back(p1);
points.push_back(p2);
points.push_back(p3);
points.push_back(p4);
std::sort(points.begin(), points.end());
while (next_permutation(points.begin(), points.end()))
doit(points[0], points[1], points[2], points[3]);
}
int
main() {
assert(point(0, 0) < point(1, 0));
assert(point(0, 0) < point(0, 1));
assert(not (point(1, 0) < point(1, 0)));
assert(not (point(0, 0) < point(0, -11)));
perm_test(point(-1, 0), point(0, -1), point(0, 1), point(1, 0));
perm_test(point(-1, -1), point(-1, 1), point(1, -1), point(1, 1));
srandom(getpid());
perm_test(point(rint(100), rint(100)), point(rint(100), rint(100)),
point(rint(100), rint(100)), point(rint(100), rint(100)));
points photo;
photo.insert(point(2,2));
photo.insert(point(3,2));
photo.insert(point(3,3));
photo.insert(point(2,3));
points trace;
trace.insert(point(-2, 0));
trace.insert(point(-2, -2));
trace.insert(point(0, -2));
points_list tracks = find_tracks(photo, trace);
assert(tracks.size() == 4);
photo.clear();
photo.insert(point(2, 2));
photo.insert(point(4, 2));
photo.insert(point(4, 3));
photo.insert(point(2, 3));
trace.clear();
trace.insert(point(-2, 0));
trace.insert(point(-2, -1));
trace.insert(point(0, -1));
tracks = find_tracks(photo, trace);
assert(tracks.size() == 2);
photo.clear();
photo.insert(point(2, 2));
photo.insert(point(2, 4));
photo.insert(point(3, 4));
photo.insert(point(3, 2));
tracks = find_tracks(photo, trace);
assert(tracks.size() == 2);
}
#endif
Defines tform.cc (links are to index).
This code is written to a file (or else not used).
<tform.h>=
#ifndef _tform_h_defined_
#define _tform_h_defined_
#include <set>
#include <vector>
// Your basic 2d point. For some reason you can't overload operator << to work
// with std::pair in g++ (ver 3.2.3 and earlier), so I have to make my own
// pair.
struct point {
double x, y;
point() : x(0.0), y(0.0) { }
point(double x, double y) : x(x), y(y) { }
};
// A point set.
typedef std::set<point> points;
typedef points::const_iterator points_citer;
// A list of point sets.
typedef std::vector<points> points_list;
// Given a particle traces, return a list of the particle tracks found in the
// given photograph.
extern points_list find_tracks(const points & photo, const points & trace);
// Return true iff the given doubles are close enough to being equal.
extern bool eq(double, double);
// Return true iff p1 is sufficiently less than p2.
extern bool operator < (const point & p1, const point & p2);
#endif
Defines point, points, points_citer, points_iter, points_list, tform.h (links are to index).
This code is written to a file (or else not used).

