Programming Assignment 2 - Graph Path Compression

See the assignment turn-in page (last modified on 3 November 2003) for instructions on turning in your assignment.

Every graph has a source node and a sink node. A source node is a node with no in edges; a sink node is a node with no out edges. In the example above, node a is the source node and node d is the sink node.

For example, the graph

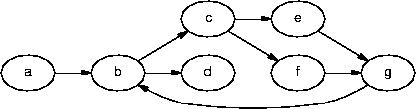
has nodes a, b, c, d, e, f, and g ; node a is the source node and node d is the sink node.

A path through a graph is a sequence of i nodes n₀, n₁, ... n_i from the graph with the following properties:

1. Node n₀ is the source node.

2. Nodes n_k and n_{k + 1} for 0 <= k < i are connected by an edge.

3. Node n_i is the sink node.

For example, the node sequence

is a path through the graph given above, while the node sequence

is not a path for the graph above because it doesn't end at the sink node, and the node sequence

is not a path for the graph above because there is no edge between nodes g and d.

A path normally contains many redundant nodes. For example, because every path starts at the source node and ends at the sink node, it isn't really necessary to include them in the path.

A compressed path is formed by deleting redundant nodes from a path. A compressed path has the advantage of being shorter than the path from which it came, but it still has all the information necessary to reconstruct the complete path.

For example, the path

can be compressed by removing the source and sink nodes:

Notice that a compressed path usually won't be a path by the definition given above; however it's always possible to recover the proper path from the compressed path.

A minimal compressed path is a compressed path with no redundant nodes. For example, the path

produces the minimal compressed path

Note that, in general, minimal compressed paths need not be unique. For example, the path a, b, c through the graph

can be represented by any of the minimally compressed paths a, b, or c.

A graph is a sequence of one or more node descriptions. Each node description is a line containing one or more node labels; adjacent node labels are separated by one or more space characters. The first (leftmost) node label is a tail node; the remaining node labels are head nodes directly connected to the tail node. Each node description follows the next with no intervening blank lines.

A path description is a sequence of node labels from the given graph; each node label is separated from the next by one or more space characters. Each line contains a single path description, and a path description is contained in a single line.

If the intput graph is incorrect, your program should output a descriptive error message end exit. If an input path description is incorrect, your program should write a descriptive error message to std-out; the error message should start with the characers "! " (that's bang followed by space).