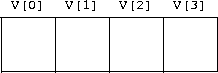
Some languages also provide a mapping in right-to-left order by decreasing negative index value.
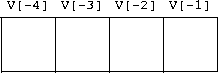
Derive the expression to map indices to array elements for right-to-left order by decreasing negative index values. Don't forget to explain your derivation. Only answer the question for 1-dimensional arrays.
Given an array of elements, each of type Etype, the non-negative index value i corresponds to the array element with a start address addri given by
(1) addri = addr0 + (i - low)*sizeof(Etype)
where addr0 is the start address of the first (or leftmost) array element and low is the corresponding index of the first array element (low = 0 in C++).
We can find the mapping for negative indices in (at least) two ways. First, we can turn around equation (1) given above so it works from right-to-left:
(2) addri = addrn-1 + (i - high)*sizeof(Etype)
Given an n-element array and a negative index value i, it computes addr, the start address if the element at index i, where addrn-1 is the start address of the last (or rightmost) array element and high is the last element's index.
Good programmers always look for ways to reuse what they've already done.
Staring at the diagrams given in the problem statement, it eventually becomes
clear that the index -1 is equivalent to the index n - 1, the index
-2 is equivalent to the index n - 2, and, more generally, the
right-to-left index j is equal to the left-to-right index n + j,
where n is the number of elements in the array. Plugging this equivalence
into equation (1) gives a second expression
(3) addri = addr0 + (n + i - low)*sizeof(Etype)
that maps a right-to-left index into an array element by first translating the right-to-left index into the equivalent left-to-right index and then uses the standard mapping equation (1).
Most people got this wrong. A few people discovered the relation between non-negative and negative indices, but stopped there without deriving a mapping expression. A couple of other people tried to answer this question with for loops.
Nyhoff complains that C-C++ arrays are not self-contained because they don't have any indication as to the number of elements in the array. You could remove Nyhoff's violation by adding a size indicator to the array, which would be tricky to do with plain-old arrays.
Most people didn't remember what Nyhoff's complaint about arrays was. A lot of people wrote it was that arrays weren't dynamically sized, which is true but not what Nyhoff was complaining about.
You should probably disagree with your colleague. Eliminating sequencing leaves
you with iteration and choice. It would be difficult, if not impossible, to
represent the sequential program S1 ; S2 ;
S3 using only loops and if statements.
On the other hand, if you were willing to loosen the definition of sequence and admit function calls, it is possible to represent algorithms without sequence. However, we're not going to come close to the machinery that allows you to do that in 305.
This was a tough one, largely because it was open ended. Mainly I was looking for a knowledge of the three control structures, but most people just agreed or disagreed with no justification to the other control structures.
element-type array-name[dim1]...[dimn];
Explain how to determine the size in bytes of the resulting n-dimensional array in memory.
The size in bytes of a one-dimensional array is given by
(1) nsizeof(EType)
where n is the number of elements in the array and EType is the array's element type. If the array's element type is itself an array, then we can repeat the formula (1) again for EType. The size of the n-dimensional array in memory is then
dim1*dim2*. . .*dimn*sizeof(element-type)
Few people got this right. Some people forgot to multiply in the element size, others didn't multiply in all the dimensions, and still others added instead of multiplied.