- Because there are five triangles and two quadrilaterals, there can be at most 5*3 + 2*4 = 23 vertices in the outline.
- Because the outline is one piece, adjacent tans must share at least one vertex, which means at least 6 and possibly more vertices are coincident, leaving at most 23 - 6 = 17 vertices in the outline.
Based on this reasoning your colleague's tangram solver checks the number of
input points and prints impossible if the number is larger then 17.
Demonstrate that your colleague's reasoning is incorrect by describing a test case that can be solved but will be rejected as being impossible by your colleague's tangram solver.
You do not need to describe the input coordinates; just describe the flaw in your colleague's reasoning and how your test case would exploit the flaw to produce incorrect results.
The second part of your colleague's reasoning is flawed: adjacent tans don't have to share any vertices, which means that a valid input may have more than 17 vertices. For example, the clearly solvable test case
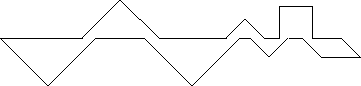
has 23 vertices.
Most people got the general idea right, but made arguments that confused the issue, or else suggested that such 17+ vertex outlines may exist without presenting one. A number of people used the candle outline as an example, but, amusingly enough, the candle outline uses 17 points.
As discussed in Section 12.3.5, when a binary operator is included in a class as a member function, the left operand is taken to be an instance of the class of which the binary operator is a member. However, the left operand of an extraction (or insertion) operator must be a stream. Including an extraction operator in the Str class wouldn't work at all, because type of the extraction operator's left operand would be wrong (A Str rather than a istream).
One, maybe two, people got this right.
= means
assignment and = means copying. In particular, for some class C, in
the following sequence
C c; c = another_C_instance;
your colleague feels that the = is a copy because c is uninitialized.
What explanation do you give to clear up your colleague's confusion?
Your colleague is confused because c is initialized by the default
constructor C::C(). Because the left-hand side of the assignment is
initialized, = corresponds to an assignment and not a copy.
A number of people argued for assignment without arguing why it should be assignment.
n is the number of elements in a, provide a worst-case
run-time asymptotic estimate of the code
find(a[], n, x)
i = 1
while i < n and a[i] != x
if a[i] >= x
i = i*2 + 1
else
i = i*2
return i
in terms of n. Carefully describe your analysis steps. For full credit
your analysis should be tight with respect to the usual family of estimate
curves; that is, for full credit, your analysis should give the curve from the
usual family of curves that is as close to the actual run-time behavior as
possible.
All the basic statements can reasonably be assumed to take constant time, giving
find(a[], n, x)
O(1)
while i < n and a[i] != x
if a[i] >= x
O(1)
else
O(1)
O(1)
The guard on the if statement takes constant time, which collapses the statement to constant time.
find(a[], n, x)
O(1)
while i < n and a[i] != x
O(1) + max(O(1), O(1)) = O(1) + O(1) = O(1)
O(1)
The guard on the while takes constant time, but the bounds on the number of
loop iterations does not. i starts at 1 and doubles (approximately) on
every iteration through the loop. The loop terminates when i is not less
than n. The loop iterations are bounded above by the smallest number of
times 2 can be multiplied by itself to produce a number not less than n;
in other words, the smallest value of j such that 2j >= n, or,
taking the log of each side, j = log n. Using this in the while rule
gives
find(a[], n, x) O(1) O(log n)*(O(1) + O(1)) = O(log n)*O(1) = O(log n) O(1)
An final application of the sequence rule gives
find(a[], n, x) O(1) + O(log n) + O(1) = O(log n)
find() runs in time O(log n) for an array of length n, and
because the usual curve family has no curves between log n and constant,
this is a tight bound.
Many people came up with an O(n) bound, which was not tight. For some reason, some people derived an O(n2) bound by assigning the if statement an O(n), which is perhaps confusing the number of times the if is executed with the time it takes to execute the if once.