Describe the input script and expected output, and explain how the expected output satisfies the required test.
One simple test is
move r0 a move b r0 move r0 c move d r0
The effect of this code is
b = a d = c
The first and second (and third and fourth) statements can't be combined because of data dependencies. The first and third statements can't be combined because they both write register 0 and combining them in a single compound statement would cause a conflict over the value written to register 0. Without register renaming the optimized code would be the same size as the input code.
However, renaming the register used in the first and second (or third and fourth) statements removes the conflict and allows the pairs to be combined:
move r0 a ; move r1 b move b r0 ; move d r1
std::remove(s, e, v) generic
algorithm is misnamed.
Because mutating generic algorithms can't change the size of a container,
std::remove() is misnamed because it can't remove anything; that is, it
can't decrease the size of a container by removing elements. For example:
std::vector<int> ivec(10, 3); std::remove(ivec.begin(), ivec.end(), 3); assert(ivec.size() == 10);
executes without error.
A lot of people answered this without providing a code sample. It's important that you, in addition to understanding the problem, actually do what the problem asks you to do.
a) for (C::iterator i = c.begin(); i != c.end(); i++)
c.erase(i)
b) C::iterator e = c.end()
while (c.begin() != e)
c.erase(c.begin());
What is the type of container C?
Loop a can never be correct, because the call to erase() invalidates
i, which makes the effect of i++ undefined. Loop b is correct as
long as erasing an element of c doesn't invalidate the iterator e.
This means C can't be a vector, but it could be a list.
a) string str2;
for (string::iterator cp = str1.begin(); cp != str1.end(); cp++)
str2 += *cp;
b) string str2;
for (string::iterator cp = str1.begin(); cp != str1.end(); cp++)
str2 = *cp + str2;
Make sure you clearly state your realistic assumptions.
In loop a the calls to the iterator member functions take constant time. The
loop body, which appends a character to the end of a string, also takes
constant time if we ignore the need to resize the string, which we can do by
assuming that str2 is properly sized before starting the loop, most likely
by executing something like
str2.capacity(str1.size())
If you don't want to assume str2 is of proper size, then you have to make
a guess as to what the resizing (and subsequent copying) behavior. One
reasonable guess is a doubling from some initial size, say 1.
To finish out loop a, it performs O(n) iterations, where n is the
number of characters in str1. Under the simpler assumption of str2
being properly sized, loop a takes O(n)*O(1) = O(n) time to execute.
In loop b the loop overhead is the same as it was for a. However, the loop
body now takes O(n) times per iteration because it has to (in effect)
push all the characters currently in str2 to the right one to make room
for the new character (here we can reasonably assume that the temporary created
to hold the new string resulting from the catenation is properly sized, and so
there's only one copy done).
Loop b also iterates the same number of times as did loop a, for an overall
estimate of O(n)*O(n) = O(n2).
Given the asymptotic estimates, loop a is faster than is loop b.
As a sanity check, this graph
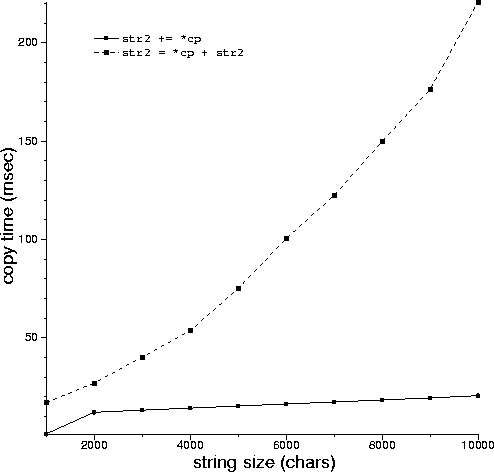
plots data generated by this program. The graph shows that 1) it more expensive to add a character to the beginning of a string than to the end, and 2) as the string size grows, the cost of adding a character to the beginning of a string grows more rapidly than does the cost of adding a character to the end of a string.