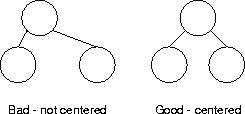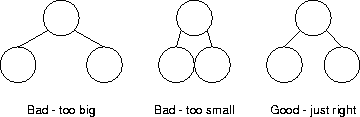This assignment is due by 2:00 p.m. on Friday, 5 October.
See the assignment turn-in page (last modified on 11 September 2001) for instructions on turning
in your assignment.
A tree is a data structure made up of nodes using the following
rules:
- A single node is a tree.
- A node owning a list of trees is also a tree (note that rule 1 is a
special case of rule 2 with an empty list of trees). The trees in the list are
called the children of the owning node; the owning node is called the
parent of the trees in the list.
The list of children imposes an order among the children; the first child in
the list is the leftmost child; the last child in the list is known as the
rightmost child.
In every tree there is a node with no parent; this is known as the root
node. A tree also one or more nodes without children; these are known as
leaf nodes. A smaller tree that is part of a larger tree is known as a
subtree of the larger tree; the children of a node are the subtrees of the
tree having their parent as its root.
Trees are easy to draw. Each node is represented as a circle. If a node has
children, the children are drawn underneath the parent in the left-to-right
order given by the list of children, and a line connects the parent to the root
of each of its children, one line per child; the lines are known as edges.
Traditionally, the root of the tree is drawn at the top of the tree, and the
leaves are drawn at the bottom of the tree.
A node's level in a tree is given by the number of edges between it and
the tree's root. The root is at level 0 (because there are no edges between
the root and the root); the root's children are at level 1, the children's
children are at level 2, and so on.
The following picture illustrates these points:
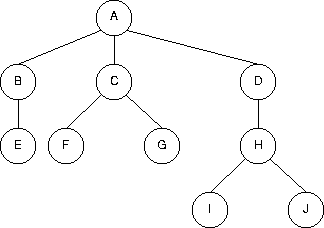
Node A is the root; nodes B, C, and D are the root's children. Nodes E, F, and
I are among the leaf nodes; the tree rooted at node H is a subtree. Node B is
at level 1; node F is at level 2, and node I is at level 3.
Before a tree can be drawn, it has to be laid-out, which involves
determining the position of the nodes relative to one another. A tree is
neatly laid-out if it is laid-out using the following rules:
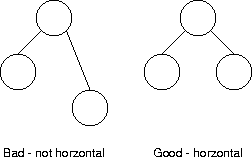
- All nodes at the same level are on a horizontal line.
- A parent is centered above its children (if any).
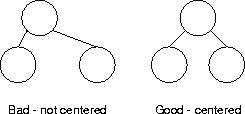
- The outline of the complete tree should occupy as small an area as
possible. On the other hand, nodes should be no closer than some user
specified minimum.
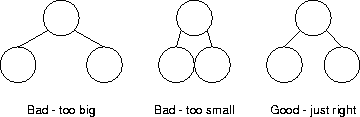
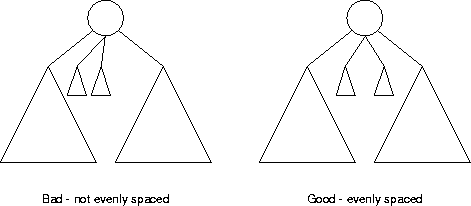
- Shorter subtrees should be evenly spaced between taller subtrees.
The example picture shown above is not neatly laid-out
because it violates rule 3: the subtree rooted at D is too far to the right and
the tree is taking up too much area.
Write a program that reads from standard-in a description of a tree and writes
to standard-out a description of the tree neatly laid-out.
The input describes one tree, and consists of a sequence of zero or more
text lines. Each text line describes a node in the tree, and has the following format:
label parent height width rest-of-line
where
label: The node's label; a single word.
parent: The label of the node's parent; a single word.
height: The height of the node; a positive integer.
width: The width of the node; a positive integer.
rest-of-line: Arbitrary data; a string.
A word is a maximal sequence of non-white-space characters. Each field is
separated from the next by one or more white-space characters (excluding the
newline, which can only occur at the end of the line); white space between
fields in excess of that needed to separate adjacent fields should be ignored.
The rest-of-line may or may not exist for each node. If it does exist, it
cannot start with white space; it may, however, end with white space. The line
ending newline character is not part of rest-of-line.
The node height and width are given in some arbitrary units called units.
Node labels are unique in a tree; if two nodes in a tree have the same label,
the input is incorrect. The root node is identified with the label root;
the parent field is ignored. Nodes appear in any order in the input; however
in which children of a parent are read from input gives the left-to-right order
of the children.
Any errors found in the input should result in an informative error message and
termination.
As an example, the following input data describes the example picture shown above:
i h 1 1
h d 1 1
e b 1 1
b root 1 1
f c 1 1
c root 1 1
j h 1 1
root root 1 1
g c 1 1
d root 1 1
Each node has height and width 1, and there is no rest-of-line data.
The output describes a neatly laid-out version of the input tree, and has
approximately the same format as the input: a sequence of lines, each having
the format
label parent height width x y rest-of-line
where
x: The x coordinate of the node's center; an integer.
y: The y coordinate of the node's center; an integer.
The remaining fields have the same description they had for input; they also
have on output the same values they had on input.
The center of the root node should be located at (0, 0). Nodes may be output
in any order.
Your program should accept the following command-line options:
-h n - Specify the minimal horizontal separation. Given two
nodes whose centers lie on the same horizontal line, the horizontal distance
between any point on the first node and any point on the second node should be
at least n >= 0 units. The default minimal horizontal separation is
n = 10 units.
-v n - Specify the vertical separation between adjacent
levels. The vertical distance between any point on a level i node and any
point on a level i + 1 node should at least n >= 0 units. The
default vertical separation is n = 20 units.
Invalid options or option values should result in an informative error message
and termination.
The program /export/home/class/cs-509/pa2/make-tree writes to standard-out a
randomly generated tree. The command format is
/export/home/class/cs-509/pa2/make-tree [n]
where n is a number used as the seed of the random number generator; the
default seed is n = 0. Different values of n should produce
different trees; the same value of n should produce the same tree.
This page last modified on 4 October 2001.